Йоганн Кеплер
|
Скачати 54.25 Kb.
|
|
| Дата конвертації | 18.08.2019 |
| Розмір | 54.25 Kb. |
| Тип | реферат |
|
|
-
Навігація по даній сторінці:
- Кеплер в Граці. «Космографіческая таємниця»
- Головний пошук. «Нова астрономія»
- Кеплерівської концепція тяжіння.
- Математичні дослідження Кеплера.
- Список використаної літератури
|
Реферат з історії механіки Йоганн Кеплер виконав: Дитинство і юність У двох десятках кілометрів на захід від Штутгарта - головного міста землі Баден-Вюртемберг (Німеччина), серед Мальовничих пагорбів неподалік від лісистого Шварцвальда розташувався невелике провінційне містечко Вейл-дер-Штадт за все з шістьма тисячами жителів. Багато що нагадує тут про давно минулі дні - давні міські стіни, середньовічні будинки, старовинна ратуша і церква з трьома шпилями. На центральній площі пам'ятник-на високому постаменті застиг з циркулем в руці літній чоловік в старовинному одязі. Розповідають, що коли в початку 1945 р до містечка підійшли французькі війська, командування вирішило піддати Вейль-дер-Штадт потужному артилерійському обстрілу, побоюючись, що за міцними стінами знайшли притулок недобиті гітлерівці. Однак вогонь так і не був відкритий: командир скасував артилерійський наліт, дізнавшись, що перед ним рідне місто Кеплера. Це обставина врятувала містечко від значних руйнувань і зберегло його Стародавній вигляд. У цьому місті (який мав тоді більш коротку назву Вейл) 27 грудня 1571 року в 2 години 30 хвилин пополудні в домі бургомістра народився Йоганн Кеплер - знаменитий астроном, фізик і математик кінця XVI - першої третини XVII ст. У ті далекі часи в містечку проживало всього близько двохсот родин бюргерів, в більшості ремісників: ткачів і шкіряників. Кеплер влаштувалися в Вейл близько 1520, коли сюди з Нюрнберга переселився прадід майбутнього астронома, кушнір Себальда Кеплер, син палітурника. У Себальда Кеплера, у свій час виконував обов'язки міського скарбника, була велика сім'я. Один з його синів, теж Себальда, одружений на Катерині Мюллер з близького містечка Марбах, був з 1569 по 1578 р бургомістром Вейля. І його бог не скривдив дітьми ¾ їх було рівно дюжина. Четвертим за старшинством був Генріх, який відсвяткував 16 травня 1571 р весілля з дочкою сільського шинкаря з сусіднього селища Ельтінгена Катериною Гульденман. Нареченому і нареченій було в той час по 24 роки. Через сім з половиною місяців після весілля у них з'явився первісток - маленький і дуже слабкий дитина, названий при хрещенні Іоганном. Про несприятливій обстановці, в якій пройшло дитинство вченого, можна судити по характеристикам, які Кеплер дав своїм найближчим родичам в фамільному гороскопі, складеному їм уже в зрілому віці, в 1597 році. Ось що він пише про свого батька: «Генріх, батько мій, народився 19 січня 1547 року. ... Людина злісний, непохитний, сварливий, вона приречена на худий кінець ..., блукач ... 1574 р мій батько вже в Бельгії. У 1575 мати відправилася до Бельгії і разом з батьком повернулася. У 1576 батько знову опинився в Бельгії, а в 1577 ... ледь уникнув небезпеки бути повішеним. Він продав свій будинок і відкрив харчевню. У 1578 ... запалилася банку рушничного пороху і занапастила обличчя батька ... в 1589 ... залишивши мати тяжко хворий, він зник з дому остаточно ... ». У такому оточенні грубих неосвічених людей пройшли перші роки життя маленького Йоганна. Його дитинство і юність були затьмарені та іншими обставинами - відсутністю належного догляду і дуже слабким здоров'ям, що призводять до частих і тривалим захворюванням. Слабке здоров'я було серйозною перешкодою для астрономічних спостережень в холодні ночі, але ще більшою перешкодою був вроджений недолік зору - сильна короткозорість і монокулярная поліопсія (множинне зір) - стан очі, зазвичай непоправне, при якому фіксується одиночний об'єкт здається множинним. Відомою компенсацією за негаразди дитинства була для Кеплера відносна доступність освіти в тодішньому Вюртемберзі. Хоча батьків, мабуть, мало турбувало освіту Йоганна, в семирічному віці (1578 р) вони помістили його в початкову німецьку школу, де навчали читання, письма та елементарних навичок в обчисленнях. Ще перед закінченням школи батьки стали думати, що робити далі з хлопчиком. Убогих і слабке здоров'я не дозволяли використовувати його на важких польових роботах. Поради вчителів, грошові міркування і в меншій мірі релігійні спонукання привели їх до вирішення вибрати для дитини духовну кар'єру. Шлях до високих духовних постам давало закінчення теологічного факультету університету, для вступу на який потрібно було закінчити нижчу і вищу семінарії. Кеплер починає навчання в 1584 році в граматичній школі (нижчій семінарії) в Адельсберге, а через 2 роки, з 26 листопада 1586, продовжує навчання у вищій семінарії в Маульбронне. Програма навчання була дуже велика: крім богослов'я, вивчалися римські і грецькі класики, риторика і діалектика, математика і музика. Режим був жорстокий: заняття в класах починалися взимку в 5 годині ранку, а влітку - в 4. 25 вересня 1588г. Кеплер витримує в Тюбінгені іспит на ступінь бакалавра, після чого ще рік продовжує навчання в Маульбронне. 17 вересня 1589 року починається його навчання в Тюбингенском університеті. Серед викладачів університету, які мали вплив на молодого Кеплера, слід зазначити професора класичної філології Мартіна Крузіуса (1526 - 1607), богослова Маттіаса Гафенреффера (1561 - 1619), пізніше ректора університету, і особливо Міхаеля Местліна (1550 - 1630). Местлін дуже скоро помітив надзвичайні здібності Кеплера до математики і астрономії, що проявлялися, зокрема, в тому, що той виводив нові теореми (як їх тоді називали - пропозиції) і робив побудови, лише потім переконуючись, що вони вже відомі. Местлін ввів молодого вченого в коло небагатьох своїх вихованців, які користувалися його особливою довірою, серед яких він пропагував коперниканское навчання. Поряд з астрономією Кеплер вже в ті роки цікавився астрологією, що для нього було не тільки даниною часу, але і відповідало його тодішнім уявленням про причинності і взаємозв'язках між явищами. Серед студентів він вважався великим майстром в складанні гороскопів. У другій половині 1594 р теологічну освіту Кеплера мало завершитися. Але в перші місяці цього року, перш ніж він зміг отримати документи про закінчення університету, які відкривали йому формально шлях до блискучої духовної кар'єри, несподівано сталися події, в результаті яких намітився вирішальний поворот у його житті і діяльності. У протестантській середній школі в Граці, головному місті австрійської провінції Штирії, помер викладач математики, вихованець Тюбінгена Георг Стадіус. Штирийская протестантська громада звернулася до сенату Тюбінгенського університету з проханням підшукати гідного наступника серед університетських вихованців. Викладачів математики в Тюбінгені, як, мабуть, і в інших тодішніх університетах, спеціально теста, і вибір сенату, не без участі Мёстліна, упав на 22-річного магістра мистецтв Йоганна Кеплера, краще за інших підготовленого до цієї діяльності. Хоч і не хотілося Кеплеру залишати навчання, а разом з нею і мрію про духовну кар'єру, а діватися було нікуди - він був зобов'язаний підкоритися з постановою сенату і вирушити за призначенням. «Я виховувався на рахунок герцога Вюртембергского і ... зважився прийняти першу запропоновану мені посаду, хоча і з не особливою полюванням», - писав він пізніше. Кеплер в Граці. «Космографіческая таємниця»
Обстановка, що оточувала Кеплера в Граці, мало сприяла його наукової діяльності. Бо, як зауважив його друг Коломан Цегантмаір, секретар барона Герберштейна, Штирийская знати виявляла разюче невігластво в усьому, мала варварської точкою зору в своїх судженнях, ненавиділа науку і нічим менше не цікавилася, ніж вченими. Предмет, викладати який належало Кеплеру, не викликав у дворянських і бюргерських нащадків ентузіазму. Вивчення математики не було, мабуть, обов'язковим, і якщо в перший рік його уроки ще відвідувало кілька учнів, то на наступний не залишилося жодного. Однак контролювали роботу викладачів інспектори виявилися досить великодушними, не ставлячи це в провину вчителю, так як, на їхню думку, на «вивчення математики всяк здатний». Натомість математики Кеплеру довелося викладати арифметику, класичну літературу (Вергілія), риторику та інші предмети. Разом з посадою викладача по існуючої традиції він набував також звання і посаду «Landschaftsmathematikus» (т. Е. Математика провінції [Штирії]), йому ставилося також в обов'язок щорічно складати календарі. У виданому в дві фарби першому календарі Кеплера містилися різні астрономічні відомості, в тому числі дані про фази Місяця, про становище планет і Сонця серед зірок, короткі статті про астрономічні і фізичних явищах. Слідуючи сталій традиції, а також піклуючись про «збереження платні, посади й даху», довелося «для задоволення безрозсудно-дурного цікавості» прикласти до календаря «Прогнози» ( «Prognostika») - види на погоду і на урожай, політичні та інші передбачення астрологічного характеру. Кеплер неодноразово дуже скептично і досить самокритично оцінював свої заняття складанням календарів і астрологією для заробітку. В одному з листів він висловлюється так: «Щоб шукає істину міг вільно віддаватися цьому заняттю, йому необхідні щонайменше їжа і дах. У кого немає нічого, той раб всього, а кому охота йти в раби? Якщо я складаю календарі та альманахи, то це, без сумніву, - прости мені, господи, - велике рабство, але воно в даний час необхідно. Боронь я себе хоч на короткий час від цього - мені довелося б йти в рабство ще більш принизливе. Краще видавати альманахи з прогнозами, ніж просити милостиню. Астрологія - дочка астрономії, хоч і незаконна, і хіба не природно, щоб дочка годувала свою матір, яка інакше могла б померти з голоду ». Вплив небесних світил на мешканців Землі Кеплер намагався пояснити в зв'язку з появою комети 1607 р наступним чином: «Якщо дійсно вірно, що згідно з порядком природи поява комети викликає, а значить і віщує такі явища, як вітер, повені, посуху, землетруси або чуму , то це повинно відбуватися таким чином: коли на небі з'являється який-небудь винятковий феномен, то життєві сили всіх природних речей повинні відчувати це. Ця симпатія, що зв'язує всі з небом, простирається особливо на силу, приховану в Землі і панівну над її внутрішнім станом. Внаслідок цього з Землі виділяються вологі випаровування, що тягнуть за собою дощі, повені, а під кінець і чуму ». Однак обмежений характер астрологічних прогнозів не раз підкреслювався Кеплером: «Той астролог, який передбачає деякі речі по небу, не враховуючи характеру, душі, розуму, сили і статури того, кому він повинен передбачити, надходить неправильно», - писав він. У той же час віра Кеплера в астрологію підтверджується багатьма фактами, і серед них такий: в січні 1598 р у нього народився син Генріх, а у Местліна - син Август. Складаючи їм гороскопи, Кеплер дійшов висновку, що обох чекає швидка смерть. Чи не спотворюючи цей страшний прогноз, він повідомляє його Местлін. Діти і справді незабаром померли, але не в назначений час. Влітку 1595 р Кеплер, як йому здалося, підійшов до великого відкриття: він вирішив, що їм виявлені найважливіші закономірності в будові, встановлена першопричина взаємного розташування планет Сонячної системи. Ще в студентські роки, познайомившись через Местліна з вченням Коперника, Кеплер став переконаним його прихильником. При цьому, однак, нове астрономічне вчення вкладалося у нього в рамки релігійної свідомості, звідки і черпалися їм джерела нових побудов. Прагнучи глибоко проникнути в таємниці будови Всесвіту, він хоче досягти цього пізнанням божественних планів творення світу. Будучи впевненим в існуванні мудрого промислу божого, він думає, що при створенні світу бог повинен був виходити з простих числових властивостей і співвідношень, використовувати вчинені геометричні форми. Цей піфагорійсько-платонівська підхід до вивчення питань світобудови ліг в основу його першого великого астрономічного дослідження, інтенсивну роботу над яким він розгорнув приблизно через рік після приїзду в Грац. У числі перших питань, що виникли перед Кеплером, був наступний: чому існує тільки шість планет, а не двадцять, або, скажімо, сто? Це питання треба було вирішити разом із поясненням відносної величини відстаней між траєкторіями руху планет.Спробою відповісти на питання такого роду почалися багаторічні дослідження, які врешті-решт привели до відкриття законів руху планет. Спочатку він припустив, що між параметрами планетних орбіт повинні бути прості співвідношення, що виражаються цілими числами. «Я витратив багато часу на це завдання, на цю гру з числами, але не зміг знайти ніякого порядку ні в численних співвідношеннях, ні в відхиленнях від них» - пише він у передмові до «Космографічні таємниці». Потім він спробував вирішити цю задачу, припустивши існування додаткових, ще не відкритих через малих розмірів, планет: одну з них він помістив між Меркурієм і Венерою, а іншу - між Марсом і Юпітером, розраховуючи, що тепер вдасться виявити бажані співвідношення, а й цей прийом не привів його до очікуваних результатів.
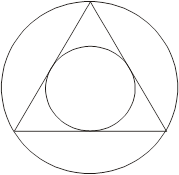
«Я витратив майже все літо на цю важку роботу, і в кінці кінців зовсім випадково підійшов до істини». 9 липня 1595 року - Кеплер скрупульозно зафіксував цю дату, - вирішуючи з учнями якусь геометричну задачу, він накреслив на класній дошці рівносторонній трикутник з вписаною в нього і описаної біля нього колами (див. Рис.1). Раптово його осяяла думка, яка з'явилася, на його думку, ключем до розгадки таємниці Всесвіту. Прикинувши відношення між радіусами кіл, він зауважив, що воно близьке до відношення радіусів кругових орбіт Сатурна і Юпітера, як вони були обчислені Коперником (тут ставлення R: r = 2: 1, а відношення R З: R Ю = 8.2: 5.2, по Копернику). Надалі хід міркувань був таким: Сатурн і Юпітер - «перші» планети (рахуючи по напрямку до Сонця) і «трикутник - перша фігура в геометрії. Негайно я спробував вписати в наступний інтервал між Юпітером і Марсом квадрат, між Марсом і Землею - п'ятикутник, між Землею і Венерою -шестіугольнік ... ». За часів Кеплера було відомо лише шість планет Сонячної системи, що спостерігаються неозброєним поглядом: Меркурій, Венера, Земля, Марс, Юпітер і Сатурн. Планета Уран була відкрита В. Гершелем багато пізніше - в 1781 р, Нептун відкритий астрономом Галле і математиком Левер'є в 1846 р, Плутон був виявлений тільки в 1930 р Але справа не ладилося, хоча, здавалося, мета була зовсім близькою. «І ось я знову кинувся вперед. Навіщо розглядати фігури двох вимірювань для пригону орбіт в просторі? Слід розглянути форми трьох вимірів, і ось, дорогий читачу, тепер моє відкриття у Ваших руках! ». Можна побудувати будь-яке число правильних багатокутників на площині, але можна побудувати лише обмежене число правильних багатогранників в просторі трьох вимірів. Такими правильними многогранниками, всі грані яких є правильними і рівними між собою багатокутниками і всі двогранні кути яких рівні між собою, є: тетраедр (4 трикутні грані), куб (6 граней-квадратів), октаедр (8 трикутних граней), додекаедр (12 п'ятикутних граней) і ікосаедр (20 трикутних граней). Важливою властивістю правильних багатогранників є існування для кожного з них вписаного і описаного куль (сфер) таких, що поверхнявписаного кулі стосується центру кожної грані правильного багатогранника, а поверхня описаного кулі проходить через усі його вершини. Центри цих куль збігаються між собою і з центром відповідного багатогранника. Ще древнім грекам було відомо, що число видів правильних багатогранників обмежується п'ятьма. Але ж і проміжків між планетами, подумав Кеплер, теж п'ять. Як важко було припустити, що це проста випадковість (до того ж умовивід спиралося на невірне уявлення про кількість планет) і як заманливо було бачити в цьому збігу мудрість творця. Відповідь на питання, чому планет шість, не менше й не більше, здавалося знайдений. Одночасно назріває і вирішення питання про відносні відстанях між орбітами планет: в сферу, на якій розташована орбіта Сатурна, вписаний куб, в нього вписана наступна сфера - з орбітою Юпітера, далі послідовно вписані тетраедр, сфера Марса, додекаедр, сфера Землі, ікосаедр, сфера Венери, октаедр, сфера Меркурія, в центрі всієї системи у коперниканцем Кеплера, зрозуміло, Сонце, і - таємниця Всесвіту розкрито, розкрито молодим учителем протестантській школи в Граці і математиком провінції Штирії.
Математичний апарат, застосовуваний в цьому випадку, досить простий, справа зводиться до обчислень залежностей між радіусами сфер, описаних навколо відповідних правильних багатогранників і вписаних в них. Нехай, наприклад, радіус орбіти Землі, а значить і відповідної сфери, дорівнює 1. Ця сфера описана навколо ікосаедра, в який вписана сфера Венери. Вирішуючи геометричну задачу на визначення радіуса сфери, вписаною в ікосаедр, і порівнюючи отриману величину з радіусом описаної навколо ікосаедра сфери Кеплер отримав співвідношення 0,762: 1. Відносні відстані до Сонця для шести планет Сонячної системи, отримані Коперником і Кеплером, і сучасні усереднені значення наводяться в таблиці:
Бачимо, що дані Кеплера вельми значно відрізняються від обчислених ще Коперником, і до того ж у всіх випадках - в бік погіршення. Пояснюючи ці розбіжності, Кеплер припустив, що кожна з планетних сфер, не будучи матеріальної, проте має деяку товщину. Закінчивши рукопис, Кеплер назвав її так: «Prodromos dissertationem cosmographicum continens Mysterium cosmographicum» - «Провісник Космографічні досліджень, що містить Космографічні таємницю». Головний пошук. «Нова астрономія» Над «Нової астрономією» Кеплер працював з невеликими перервами з 1600 по 1606 р Значення цієї книги полягає перш за все в тому, що в ньому дано висновок двох із трьох знаменитих законів руху планет, названих його ім'ям. У сучасному формулюванні ці закони зазвичай звучать так: I. Всі планети рухаються по еліпсам, в одному з фокусів яких (загальному для всіх планет) знаходиться Сонце. II. Площі, описувані радіусами-векторами планет, пропорційні часу. Третій закон був опублікований Кеплером пізніше, в 1619 р в книзі «Harmonices Mundi» ( «Гармонія світу»). Кеплерова твір і за формою і за змістом значно відрізняється від багатьох наукових трактатів того часу. Якщо Коперник, Галілей і Ньютон знайомлять нас тільки з кінцевими результатами своїх наукових досягнень, то Кеплер цілком свідомо описує хід своєї роботи у всіх деталях, включаючи всі невдачі і успіхи, помилки і геніальні здогадки, пастки і їх обходи. Чому він так чинить, він пояснює в передмові: «Для мене важливо не просто повідомити читачеві, що я повинен сказати, але перш за все ознайомити його з доводами, застереженнями, щасливо подоланими небезпеками, які привели мене до моїх відкриттів. Коли Христофор Колумб, Магеллан і португальці, у тому числі перший відкрив Америку, другий Китайський океан, а останні - морський шлях навколо Америки, оповідають, як вони збивалися зі шляху і блукали в своїх подорожах, ми не тільки прощаємо їм це, але, більш того , ми не бажаємо пропуску цих оповідань, так як тоді при читанні було б втрачено враження про всім значному у їхніх підприємствах. Нехай же тому й мені не поставлять в провину, коли я, викликаючи у читача інтерес, піду подібним шляхом в своєму викладі. Звичайно, при читанні, наприклад пригод аргонавтів, ми самі не беремо участі в їх поневіряння, а труднощі і терни на моєму уявному шляху можуть зачепити і самого читача, але така вже доля всіх математичних творів ». Кеплер почав своє дослідження складанням на підставі спостережень Тихо Браге повного списку моментів, довгот і широт для всіх протистоянь планети Марс з 1580 року (Бразі спостерігав протистояння Марса десять разів з 1580 по 1600 р два рази - в 1602 і 1604 рр. Їх спостерігав Кеплер). Ще Коперник, слідуючи Птолемею, вважав центр земної орбіти істинним центром орбіт всіх планет. Бразі також визначав протистояння планети як становище, протилежне цієї точці, т. Е. Так званого «середнього Сонця». Кеплер вже в «Космографічні таємниці» вказував, що Сонце саме є природним центром планетної системи, і вважав, що протистояння слід брати по відношенню до реального, а не до середнього Сонцю. Це було першим істотним нововведенням в методи дослідження. Кеплер вперше припустив, що рух планет відбувається внаслідок впливу на них якоїсь сили, що виходить від Сонця. Таким чином, у Кеплера Сонце стає не тільки джерелом світла і тепла для всієї планетної системи, але також і джерелом рушійною планети сили. Друге нововведення Кеплера полягало в наступному. Орбіти всіх планет лежать не зовсім в одній площині - їх площині утворюють одна з іншого невеликі кути (наприклад, площини орбіт Землі і Юпітера становлять кут в 1 ° 18,5 '). Якщо не врахувати цей факт, доводиться зустрічатися з великими труднощами при поясненні деяких особливостей в можна побачити з Землі положеннях Марса. Коперник, наприклад, вважав, що площину орбіти Марса коливається в просторі, не цікавлячись фізичної причиною такого дивного явища. Припустивши, що справа тут в наявності деякого постійного кута між площинами планетних орбіт, Кеплер без особливих зусиль, за даними спостережень Бразі, переконується в правильності своєї гіпотези і знаходить кут між площинами орбіт Землі та Марса рівним 1 ° 50 '. Третє нововведення Кеплера більш радикально. Від Платона і Птолемея до Коперника і Бразі астрономи були впевнені в тому, що планети роблять свої кругові рухи з рівномірною швидкістю. Кеплер, зберігаючи на перших порах рух круговим, відкидає аксіому рівномірного руху. І при цьому він керується насамперед фізичними міркуваннями: якщо Сонце управляє рухом, є його джерелом, то його сила повинна діяти на планету інтенсивніше, коли вона знаходиться ближче до джерела, і менш інтенсивно, коли планета від нього віддалиться, отже, планета буде рухатися з більшою або меншою швидкістю в залежності від її відстані до Сонця. Ця ідея була не тільки запереченням античної традиції, вона відкидала і припущення Коперника, по якому не могло бути, «... щоб просте небесне тіло нерівномірно рухалася однієї сферою ...». Коперник був в свою чергу рішуче не згоден з вченням Птолемея про те, що планети рухаються рівномірно не навколо центрів своїх орбіт, а навколо уявної точки на деякій відстані від центру. Ця точка називалася punctum aequans або aequant (зрівнює точкою, або еквантом). Коперник, відмовившись від Птолемеєва еквантов, ввів замість них додаткові епіцикли. Кеплер, відкидаючи догму рівномірного руху, повернувся до поняття екванта, розглядаючи його як важливе обчислювальний засіб. Цими нововведеннями Кеплер кілька полегшив майбутнє рішення свого завдання.Кеплер писав: «Ох, скільки я повинен був пролити сліз над зворушливим старанням Апіа, який, слідуючи Птолемею, даремно витрачав свій дорогоцінний час і винахідливість на побудова спіралей, петель, гвинтових ліній, завитків і цілого лабіринту інволюцій, щоб зобразити те, що існує тільки в уяві і яке природа відмовляється прийняти як свою подобу ».
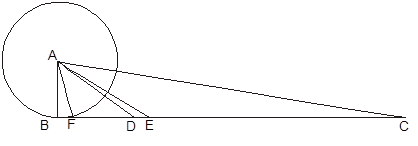
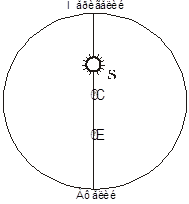
Перша спроба вирішити задачу описується Кеплером в XVI главі «Нової астрономії». Його завдання полягало насамперед у визначенні деяких параметрів орбіти Марса, яку, нагадаємо, Кеплер поки що думав кругової. Потрібно було визначити радіус орбіти (див. Рис. 3), напрямок по відношенню до нерухомих зірок лінії аспид, тобто осі, що з'єднує точку, в якій планета буває найближче до Сонця (перигелій), і протилежну їй точку (афелій), а також положення Сонця (S), центру орбіти (C) і екванта (Е), які лежать на цій осі. З журналів спостережень Тихо Браге, якими він тепер мав, він вибрав запис про чотирьох спостерігалися протистояннях Марса - в 1587, +1591, 1 593 і тисячі п'ятсот дев'яносто п'ять рр. На самому початку своїх обчислень Кеплер через неуважність допускає кілька помилок, які повинні були б істотно вплинути на правильність обчислень. Кеплер так і не помітив їх до кінця своєї роботи, але їх виявив французький історик астрономії Деламбр. Проте виправлені Деламбром обчислення в результаті дали майже ті ж значення - виявилося, що в самому кінці обчислень Кеплер під час ділення знову допустив помилки, що перекрили перші! В результаті обчислень Кеплер отримав повний ексцентриситет, рівний 0,18564 часток радіуса, причому Сонце відстоїть від центру на 0,11332, а еквант - на 0,07232 частки радіуса (сучасна теорія показує, що обидва відстані повинні бути приблизно рівні 0,5625 і 0,4375 повного ексцентриситету; значення, отримані Кеплером - 0,6104 і 0,3896 відповідно). Довгота Офелія для 1587 р становила 148 ° 48'55 ''. Отримані ним значення при підстановці в дані десяти спостережень Бразі розходилися менш ніж на 2 ', що було цілком допустимим. Однак вже наступна глава починається здивованим вигуком: «Як же це могло бути? Гіпотеза, яка добре узгоджується зі спостереженнями протистоянь, все ж є хибною ». І в двох наступних розділах Кеплер грунтовно пояснює, як він встановив, що гіпотеза помилкова і чому її потрібно відкинути. Намагаючись застосувати свою модель до обчислення проміжних положень Марса за даними спостережень Бразі, Кеплер виявляє розбіжність теорії з практикою, що досягає в чисельному вираженні 8 '. Наступний етап досліджень Кеплер описує в книзі третій. Багаторазові обчислення кажуть Кеплеру про те, що неможливо побудувати кругову орбіту планети, яка повністю відповідає даним спостережень. Окружність повністю визначається завданням трьох точок на ній, будь-яка інша крива лінія вимагає знання становища більшої кількості точок на ній. Для визначення форми орбіти Марса, шахта скоро вона не була окружністю, потрібно перш за все уточнити орбіту небесного тіла, на якому розміщений спостерігач, т. Е. Самої Землі. Адже з неправильного уявлення про рух спостерігача висновки про рух спостережуваних об'єктів будуть теж невірні. Якби було можливо в кожен момент часу знаходити безпосередньо величину відрізка Земля - Сонце. Але такої можливості у Кеплера не було. Інший принципово можливий випадок полягає у виборі в просторі деякого нерухомого орієнтиру про яку відомо, що він протягом тривалого часу зберігає своє становище незмінним. Тоді земні спостерігачі могли б при необхідності візувати напрям на нього.
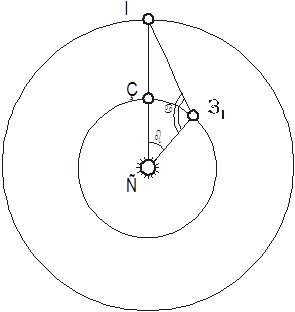
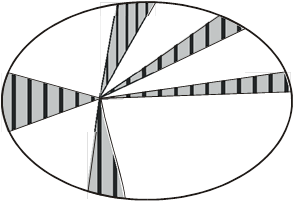
Припустимо, що в певний момент часу Земля (З) знаходиться на прямій, що з'єднує Сонце (С) з нашим орієнтиром М (див. Рис. 4). Якщо в цей час візувати з Землі напрям на орієнтир М, то отримаємо напрям СМ (Сонце-орієнтир). Нехай цей напрямок зафіксований на небосхилі. Розглянемо положення Землі в інший момент (З 1). Якщо і Сонце (С) і орієнтир М видно з Землі (З1) то в трикутнику СЗ 1 М відомий кут a = СЗ 1 М. Напрямок прямий РМ щодо нерухомих зірок визначено раз і назавжди. Але тепер, встановивши напрям на Сонце З 1 З прямим наглядом, можна визначити і кут b = З 1 СМ. Отже, трикутник СЗ 1 М може бути тепер побудований за боці РМ та двом кутках a і b для кожного положення З 1 і при цьому визначиться це саме положення З 1 щодо заданого базису РМ. Таким чином можна отримати необхідну кількість точок, що належать орбіті Землі. Але де ж взяти орієнтир М? Винахідливий розум великого астронома використовував орієнтир, хоч і не строго нерухомий, але періодично, через відомі заздалегідь інтервали часу, який займає одне і те ж положення в просторі. Справа в тому, що вже й тоді була досить точно відома тривалість марсіанського року, т. Е. Період обертання Марса навколо Сонця, - 687 днів. Використовуючи цю величину як вихідної, тепер достатньо було врахувати, що будь-який зафіксоване положення Марса (і довжина відрізка МС) через ціле число марсіанських років буде повторюватися, в той час як положення Землі на її орбіті кожен раз буде, взагалі кажучи, іншим. Таким чином можна встановити таку кількість точок орбіти Землі. Природно, що, чи не мав у своєму розпорядженні Кеплер даними багаторічних спостережень Бразі за Марсом, швидке вирішення цього завдання виявилося б неможливим. Результати проведених Кеплером обчислень збіглися з його припущеннями: Земля, як і інші планети, усупереч поширеній думці Коперника і його попередників, що не рухається рівномірно, а швидше, коли вона ближче до Сонця, і повільніше, коли далі від нього. Так вперше в історії астрономії була показана помилковість арістотелівського уявлення про рівномірних рухах планет. Далі, займаючись обчисленням відстані Марс - Земля, Кеплер знайшов, що найбільша відстань, в афелії (в частинах радіуса земної орбіти), становить 1,6678, а найменше, в перигелії, 1,3850. Тоді радіус орбіти Марса буде дорівнює:
а відстань Сонця від центру орбіти Марса
тобто половині раніше виведеного з руху Мара повного ексцентриситету його орбіти (рівного 0,1856). Таким чином Кеплером було встановлено, що повний ексцентриситет планет ділиться центром орбіти на дві рівні частини між Сонцем і еквантом. Кеплерівської концепція тяжіння. Протягом багатьох століть в природознавстві панувала аристотелевская точка зору на природу тяжіння: «Земля і Всесвіт мають загальний центр; важке тіло рухається до центру Землі, і відбувається це внаслідок того, що центр Землі збігається з центром Всесвіту ». У «Новій астрономії» на думку Кеплера, тяжіння - це «взаємне тілесне прагнення подібних (родинних) тіл до єдності чи з'єднанню». В примітках до свого пізнішого твору про місячну астрономії Кеплер пише: «Гравітацію я визначаю як силу, подібну магнетизму - взаємному тяжінню. Сила тяжіння тим більше, ніж обидва тіла ближче одне до іншого ... ». Цим самим Кеплер істотно просувається в напрямку, який пізніше призводить Ньютона до відкриття його знаменитого закону всесвітнього тяжіння. Тут же Кеплер додає: «Причини океанських припливів і відливів бачимо в тому, що тіла Сонця і Місяця притягають води океану за допомогою деяких сил, подібних магнетизму». Намагаючись встановити кількісну залежність між силою тяжіння і відстанню, Кеплер припустив, що сила тяжіння прямо пропорційна вазі, але обернено пропорційна відстані. Увага Кеплера було залучено і до такого властивості матеріальних тіл, як інерція. Сам термін «інерція» був введений в саме Кеплером. Він позначив їм явище опору руху покояться тел. Інерція руху, по крайней мере до 1620 р їм не розглядається. Важливо відзначити, що поняття інерції було поширено Кеплером (в його розумінні) на позаземні тіла і явища. У «Новій астрономії» він пише: «Планетні кулі повинні бути по природі матеріальні ..., вони мають схильність до спокою, або відсутності руху».
Для пояснення ексцентричності орбіт Кеплер припустив, що планети є «величезні круглі магніти», магнітні осі яких зберігають постійне напрям, подібно осі дзиги. Отже, планети будуть періодично то притягатися ближче до Сонця, то відштовхуватися від нього, відповідно до розташування їх магнітних полюсів. Далі Кеплер ділить всю орбіту Землі на 360 частин, відзначивши на орбіті становище Землі З1, З2,..., З 360 до відповідних моменти часу t 1, t 2,..., t 360. Кеплер зіставляв суму відстаней між Землею і Сонцем в моменти часу t i і t k (і в усі проміжні моменти) з проміжком часу, необхідним планеті, щоб перейти з положення З i, З k. При додаванні виявилося, що ця сума відрізків не залежить від обраної ділянки орбіти, а тільки від величини проміжку часу. Згадавши потім, як Архімед для знаходження площі круга розкладав його на велике число трикутників, Кеплер заміняє суму відстаней площею сектора, описаного радіусом-вектором точки орбіти, вважаючи ці величини пропорційними, хоча і не говорячи про це прямо (див. Рис. 5). Необхідно зауважити, що при виведенні закону площ (в кінці 1601 - початку 1602 г.) Кеплер зустрівся і по-своєму впорався із завданням, що має пряме відношення до того розділу математики, бурхливий розвиток якого незабаром ознаменувало настання нового етапу в історії математики, пов'язаного з обчисленням нескінченно малих. Його спроба нескінченного підсумовування по суті була першим кроком в чисельному інтегруванні. Другий закон визначав зміна швидкості руху планет по їх орбіті, проте сама форма орбіти залишалася ще невідомої. Тепер Кеплеру належало дати математичний опис тієї кривої, по якій рухається планета, і ця задача виявилася найскладнішою і трудомісткою. Довелося перевіряти одну за одною багато гіпотез. При цьому, правда, в розпорядженні Кеплера вже був потужний засіб дослідження - його закон площ. Це давало можливість, задаючи гіпотезу про криву тієї чи іншої форми, обчислювати положення, які мав би займати Марс на цій передбачуваної орбіті в різні моменти часу, і порівнювати їх з спостерігаються положеннями. «Правда лежить між колом і овалом, начебто орбіта Марса є точний еліпс». Але, помістивши Сонце в його центр, Кеплер знову не прийшов до согласующемуся з даними спостережень результату. На початку 1605 р Кеплеру вдалося знайти справжню зв'язок між відстанню Сонце - Марс і так званої ексцентричної аномалією. Він знайшов тоді рівняння, яке зараз називається його ім'ям і широко використовується в теоретичній астрономії. Це рівняння має вигляд:
Закони Кеплера зберігають своє значення і в наш час. Правда, будучи абсолютно суворими математичними законами для руху двох матеріальних тіл (точніше - матеріальних точок), вони не враховують впливу на кожну планету інших планет, які хоча і дуже слабкі, але все ж приводять до невеликих відхилень їх руху від еліптичної орбіти. Але математики та астрономи навчилися враховувати ці впливи (завдяки чому, між іншим, були відкриті планети Нептун і Плутон). Третій закон руху планет Кеплер вивів значно пізніше (в 1619 г.). Суть цього закону була викладена в праці за назвою «Світова гармонія». Кеплер формулює цей закон так: «... відношення між періодами звернення якихось двох планет саме дорівнює полуторним ступеня відносини їх середніх відстаней; однак звертаю увагу на те, що середнє арифметичне обох діаметрів еліптичної, орбіти трохи менше найдовшого діаметра ». Зараз цей закон формулюється в такій формі: квадрати сидеричних періодів планет ставляться між собою, як куби їх середніх відстаней від Сонця. Математичні дослідження Кеплера.
З 1594 р Кеплер мав офіційне звання математика: штирийский провінційний математик з 1594 по 1600 р імператорський математик із 1601 р до кінця життя і, крім того, математик провінції Верхній Австрії з 1613 по 1628 року в ті часи поняття «математика »був значно ширше ніж в наш час. Так в «Математичному словнику» французького академіка Ж. Озанама, виданому у 1691 р, крім традиційних арифметики, алгебри, геометрії, в коло математичних предметів включені були також механіка з гідростатики, архітектура і фортифікація, географія і навігація, астрономія, оптика, а також музика. У роботах Кеплера математичного характеру чітко простежується вплив, який чинили на формування нових математичних ідей і методів потреби точного природознавства, особливо астрономії, механіки. Математика за часів Кеплера ставала потужним інструментом вивчення і відкриття закономірностей і властивостей навколишнього світу. Завдання з «Нової астрономії» були лише першим його кроком у розвитку математики змінних величин. Наступним кроком була книга «Nova stereometria doliorum vinariorum ... accesit Stereometriae Archimedae Supplementum» ( «Нова стереометрія винних бочок ... з приєднанням доповнення до Архимедовой стереометрії»). Книга ця зайняла чільне місце в історії математики і, до речі, є єдиним твором Кеплера, повністю переведеним на російську мову. Книга вийшла в Лінці в 1615 року, але написана вона була майже на два роки раніше, і послужив цьому вельми цікавий привід, відомий за словами самого Кеплера. Восени 1613 року в Верхній Австрії було зібрано особливо рясний урожай винограду. Численні судна та баржі, завантажені вином, йшли вгору по Дунаю, а пристань в Лінці все ще була забита бочками. Кеплер як вирішив запастися приємним напоєм. Бочки з вином були доставлені до нього на подвір'я, а потім з'явився купець і за допомогою єдиного інструменту - мірної лінійки, стрижня з поділами, швидко виміряв кількість вина в кожній з бочок без всяких обчислень і обліку форми бочок. Він вставляв лінійку в наливний отвір бочки аж до упору в нижній край днища, після чого оголошував кількість амфор (судин, прийнятих за міру місткості) в ній. Кеплер був дуже здивований цим: яким чином похилий відрізок між двома певними точками може бути мірою місткості бочки. Він навіть засумнівався в правильності такого методу вимірювання, так як уявлялося, що дуже низька, обмежена широкими днищами, бочка могла мати таку ж відстань до нижньої точки днища, як і більш висока бочка з менш широкими днищами. Чи обґрунтовано таке визначення місткості? Тим більше Кеплер згадав, що на північ від, на Рейні, місткість бочок визначалася або безпосереднім підрахунком кількості одиниць заходи ємності при переливанні, або виробляли численні виміри розмірів бочки, після чого в результаті громіздких й обтяжливих обчислень оголошували її ємність, хоча багатьом цей спосіб здавався ненадійним. Дізнавшись, що вживання мірної лінійки санкціонується тут владою, Кеплер «вважав для себе гідною кандидатурою взяти новий предмет математичні занять і досліджувати геометричні закони такого зручного і вкрай необхідного в господарстві виміру, а також з'ясувати його заснування, якщо такі є». Уже до кінця того ж року після кількох тижнів роботи було готове твір про результати цього дослідження, і Кеплер відправив його для видання в Регенсбург, так як в цей час в Лінці ще не було жодної друкарні. Однак видавець, до якого Кеплер звернувся, невдовзі повідомив, що, на думку книгопродавців, запропоноване Кеплером твір, до того ж написаний латинською мовою, користуватися попитом не буде, і субсидувати видання відмовився. Рукопис надовго застрягла в Регенсбурзі, і Кеплер згадав про неї тільки тоді, коли за його участі навесні 1615 року в Лінці було створено друкарня. Не без труднощів (видавець, якому була спрямована рукопис, на той час помер) вдалося розшукати і повернути рукопис в Лінц. Кеплер піддає її суттєвої переробки, а також дописує нову, дуже важливу главу «Доповнення до Архімеда». Уже восени 1615 г. «Нова стереометрія винних бочок» - перша книга, надрукована в Лінці, надійшла в продаж на ярмарку в найбільшому тодішньому центрі книготоргівлі - Франкфурті. Її видання було зроблено Кеплером за свій рахунок. Намагаючись хоча б частково покрити понесені витрати, він звертається до своїх друзів з проханням рекомендувати його книгу зацікавленим особам та навчальним закладам. Про попит на математичну літературу в той час свідчить лист до Кеплеру Гданського математика Крюгера, в якому він пише, що в усій окрузі вбачає лише трьох потенційних покупців: свого Кенігсбергзького колегу, Кенігсбергськая бібліотеку і якогось дворянина на прізвище Невешінскій. Місцева влада поставилися до виконаної Кеплером роботи дуже холодно, недвозначно давши йому зрозуміти, що було б краще «цю роботу залишити, а довести до кінця важливіші речі, такі, як доручені йому« Рудольфінскіе таблиці »і географічну карту». Однак Кеплер не послухав цього досить категоричній раді і взявся за переробку своєї книги, ставлячи на цей раз метою зробити її доступною для широких кіл людей, які потребують розроблених їм прийомах у своїй практичній діяльності, але не знають латині і не розбираються в тонкощах математики. З цією метою Кеплер спрощує виклад, змінює послідовність розташування матеріалу, докладає відомості про системи заходів, древніх і вживалися в той час, а також таблиці їх перекладу з однієї в іншу, але головне - він переводить свій твір на німецьку мову. Остання обставина була дуже важливим, оскільки наукових книжок німецькою мовою тоді видавалося мало, а математична термінологія майже не була розроблена. Тому значення з'явилася вже навесні 1616 року на книжковому ярмарку у Франкфурті книги під назвою: «Ausszug auss der uralten Messekunst Archimedis», т. Е. «Вилучення з давнього мистецтва виміру Архімеда ...», полягає не тільки в залученні уваги до можливостей математичних методів широких верств населення, а й у виконаній тут велику роботу зі створення німецької математичної термінології. Цим самим, а також виданням кількох трактатів астрономічного змісту рідною мовою (і підготовкою декількох рукописів, що залишилися невиданими) Кеплер вніс істотний внесок в розвиток мови німецької природничо літератури. Книга «Нова стереометрія» складалася з трьох частин. У передмові Кеплер пише: «Оскільки ... винні бочки пов'язані з колом, конусом і циліндром - фігурами правильними - тим самим вони піддаються геометричним вимірам, принципи яких варто привести на початку цього дослідження, як вони встановлені Архімедом, звичайно лише настільки, наскільки цього досить для задоволення розуму, люблячого геометрію, а повні і в усіх частинах строгі докази слід шукати в самих книгах Архімеда, якщо хто не злякається тернистого шляху їхнього виконання. Втім, на деяких мостах, які не зачепила Архімед, потрібно зупинитися детальніше, щоб і більш вчені люди знайшли ніж скористатися і чому порадіти ». Таким чином Кеплер підкреслює, що в силу практичної спрямованості своєї праці він не затримується на положеннях свого великого попередника, відсилаючи більш вимогливих читачів до першоджерел, але тут же він говорить і про те, що виходить за межі досягнутого Архімедом.
Перша частина твору, що її названо «Стереометрія правильних кривих тіл», в свою чергу складається з двох частин, в першій з яких - «Архимедовой стереометрії» Кеплер наводить 16 теорем, відомих ще Архімед, але відмінність в підході Кеплера і підході Архімеда до вирішення відповідних завдань стає помітним з самого початку. Зупинимося на прикладі з площею кола. Твір Архімеда «Вимірювання круга» починається таким реченням: «Всякий коло дорівнює прямокутного трикутника, причому радіус кола дорівнює одній з прилеглих до прямого кута сторін, а периметр - основи трикутника». Ця пропозиція Архімед доводить побічно (методом вичерпування), показуючи за допомогою вписаних і описаних правильних багатокутників, що площа кола буде не більше і не менше площі зазначеного трикутника. Кеплер розмірковує так: «Архімед користується непрямим доказом, що призводить до неможливості, про що багато і багато писали. Мені ж здається, що сенс цього [докази] наступний: окружність кола містить стільки ж частин, скільки точок, саме, нескінченне число. Кожну з них розглянемо як підставу деякого рівнобедреного трикутника зі стороною АВ, і таким чином в площі кола виявиться безліч трикутників, з'єднаних вершинами в центрі А. Нехай, далі, окружність кола витягнута в пряму, і нехай їй дорівнює ВС, а АВ до неї перпендикулярна (див. Рис. 6). Тоді підстави всіх цих незліченних трикутників, або секторів, будуть представлятися розташованими один за одним по прямій ВС; нехай одне з таких підстав буде BF, і яке-небудь рівне йому - DЕ. З'єднаємо точки F, Е, D з А. Таких трикутників ABF, АDЕ над прямий ВС вийде стільки ж, скільки секторів в площі кола, і їх підстави BF, DЕ і загальна висота АВ будуть такі ж, як у секторів; отже, всі ці трикутники ABF, АDЕ і т. д. будуть рівновеликі (між собою) і кожен з них буде рівновеликий відповідного сектору кола. А значить, і всі разом ці трикутники, що мають підстави на лінії ВС, т. Е. Трикутник ABC, усіма ними складений, буде рівновеликий сумі всіх секторів кола, т. Е. Складеної ними площі кола. Це саме та має на увазі архимедова приведення до безглуздості ». Архімед дійсно міг мати це на увазі. Але з огляду на, що між елементарним круговим сектором і елементарним трикутником є то відмінність, що дуга в підставі сектора і радіус кола будуть при кінцевому n завжди більше відповідних ліній елементарного трикутника, для точності виведення слід показати, що різниця між площами кола і трикутника при збільшенні числа поділів може стати дійсно менше будь-якого даного як завгодно малого числа (т. е. що ця різниця є нескінченно мале). Архімед своїми міркуваннями це показує, Кеплер - немає. У Кеплера хорди окружності переходять в точки, кожна з яких продовжує розглядатися як підстава деякого рівнобедреного трикутника. Виходить, що площа кола розглядається Кеплером як якась сума всіх радіусів, а трикутника - як сукупність точок всіх прямих, що виходять з однієї з його вершин. Викладаючи завдання з творів Архімеда, Кеплер не користується архімедовим методами доказів, а застосовує підсумовування нескінченно великого числа «актуалізованих» нескінченно малих.Кеплер каже, що куля «як би» містить нескінченно багато конусів, вершини яких лежать в центрі, а підстави - на поверхні кулі, і знаходить таким чином його обсяг. Взагалі з його неодноразового «як би» ( «veluti») видно, що він не прагне дати точне доказ, а апелює тільки до наочності. У деяких місцях Кеплер цурається доказів Архімеда, називаючи їх надзвичайно глибокими, але важкими для розуміння, і замість них призводить міркування, які встановлюють «ймовірність» того чи іншого пропозиції з міркувань індуктивного або интерполяционного характеру. Так Кеплеру вдалося подолати недоліки методу вичерпання древніх. Йому, зрозуміло, не було відомо зміст архімедовим «Послання до Ератосфену», виявленого тільки в 1906 р З «Послання» стає ясно, що і Архімед користувався інфінітезімальньмі міркуваннями, досить близькими до кеплерова. Кеплер, як його сучасник Кавальєрі і інші більш пізні математики XVII в. (Наприклад, Паскаль), часто вживав вираз «Summa omnium» - «сума всіх» (сума всіх радіусів-векторів, сума всіх ординат), яке виконувало тоді роль нашого терміна «інтеграл». До речі, як відомо, знак інтеграла (подовжена буква S) був введений Лейбніцем в кінці XVII ст. саме для скороченого запису виразу «Summa omnium». У другій половині першої частини своєї роботи - в «Додатках до Архімеда» - Кеплер показує, що його спосіб виявляється дуже зручним для вирішення багатьох нових завдань. Так, в теоремі 18, наприклад, він легко встановлює, що обсяг тора дорівнює обсягу циліндра, підставою якого служить меридиональное перетин тора, а висотою - довжина кола, описуваної центром утворить тор кола. Кеплер доводить це так: меридіональними перетинами тор розбивається на нескінченно велике число кружечків, товщина яких у зовнішнього краю тора більше, ніж у внутрішнього, але товщина кружечка в центральній частині дорівнює середньому арифметичному товщини у країв. Тому Кеплер приймає, що обсяг такого кружечка дорівнює обсягу циліндра, висота якого дорівнює товщині центральній частині гуртка, а в основі лежить утворює тор коло. При цьому тор і циліндр, про які йдеться в умові теореми, розбиваються на рівне число рівновеликих частин, цим і доводиться теорема. У наступному, більш складному прикладі визначається обсяг «яблука». Так називає Кеплер тіло, утворене сегментом, великим, ніж півколо, при його обертанні навколо хорди. Дотепним перерозподілом деформованих без зміни обсягу часткою «яблука», освічених по одному способу меридіональними перетинами даного тіла обертання, що проходять через його вісь, так звану хорду сегмента, а по іншому - тонкими концентричними циліндричними шарами, що мають віссю хорду сегмента і розгорнутими в прямокутники, Кеплер отримує тіло, що представляє собою «циліндричне копито» - циліндричний сегмент, підставою якого є утворює «яблуко» сегмент, а висота дорівнює довжині окружності еква ора даного тіла обертання. Розглянувши в теоремах 18-22 питання про знаходження обсягів тора, «яблука» і «лимона» ( «лимоном» названа тіло, утворене обертанням сегмента, меншого, ніж півколо, навколо хорди), Кеплер знаходить далі об'єми та інших тіл, одержуваних при обертанні по-різному розташованих відрізків дуг конічних перетинів - еліпса, параболи і гіперболи. Всього сам Кеплер налічує 92 форми таких тіл, багатьом з яких він приписує влучні назви: «айва», «зливу», або «олива», «суниця», «груша» і т. Д. Друга частина його книги, названа «Спеціальна стереометрія австрійської бочки», починається міркуванням про геометричній формі бочок. Він вказує, що в першому наближенні бочку можна розглядати як циліндр, або як два усічених конуса, складених більшими підставами. Більш точно форма бочок відповідає середньому прошарку або лимона, освіченого сегментом кола, або сливи, освіченою частиною еліпса, або параболічного веретена, що залишається після відсікання, рівних частин по обидва боки. Далі Кеплер розглядає залежність між обсягом бочок і довжиною заміряти відрізка і відносини більшого діаметра (в середньому перерізі) до меншого. Але головний інтерес для нас представляє те, що Кеплер займається тут дослідженням форми конусів, циліндрів, а також бочок, які мають найбільшої місткістю при найменшій витраті на них матеріалу, що призводить його вже до завдань іншого найважливішого розділу обчислення нескінченно малих - диференціального обчислення: до визначення максимумів і изопериметрической задачі. Кеплер правильно зазначає основна ознака максимуму в тому, що, як він пише, різниця між самим максимумом і безпосередньо попередніми чи наступними значеннями непомітна. У третій частині книги ( «Вживання всієї книги про бочках») Кеплер дає практичні рекомендації по вимірюванню обсягів бочок, намагається знайти спосіб для визначення за допомогою мірного стрижня «відносини порожній частини до залишку рідини при лежачої бочці», але в загальному вигляді рішення цього завдання йому не вдається. Хоча інфінітезимального роботи Кеплера фактично відкрили нову епоху, новий період у розвитку математики, вони не були спочатку правильно оцінені багатьма його сучасниками. Деякі математики різко виступили проти його «нестрогих» методів визначення обсягів, проти його методу підсумовування нескінченно малих. Учень Вієта шотландець А. Андерсон вже через рік після появи «стереометрії» видав спеціальне твір «На захист Архімеда», де звинувачував Кеплера в образі пам'яті великого вченого. Вони не розуміли, що при всій Нестрогие методів Кеплера, очевидною і для нього самого, ці методи були досить продуктивні і перспективні. Таким чином, розглянуті роботи Кеплера стали початком цілому потоку досліджень, увінчалися в останній чверті XVII ст. Оформленням в працях І. Ньютона і Г. В. Лейбніца диференціального й інтегрального числення. Список використаної літератури: 1. Білий, Ю.А. Йоганн Кеплер. Вид. «Наука». М. 1971 2. Веселовський, І.М. Нариси з історії теоретичної механіки. Вид. "Вища школа". М. 1974 3. Григорян, А.Т. Механіка від античності до наших днів. Вид. «Наука». М. 1974 4. Кудрявцев, П.С. Історія фізики і техніки. М. 1960 5. Моісеєв, Н.Д. Нариси розвитку механіки. Вид. Московського Університету. тисячу дев'ятсот шістьдесят-один 6. Спаський, Б.І. Історія фізики. Вид. Московського Університету. тисяча дев'ятсот п'ятьдесят-шість |

 Мал. 4
Мал. 4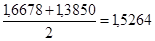
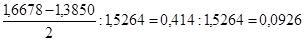
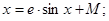
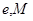 - константи.Це рівняння є одним з перших трансцендентних рівнянь, які знайшли практичне застосування. Нарешті Кеплер помітив, що бічне стиснення орбіти становить 0,00429 частки радіуса, що точно дорівнює половині квадрата певного ним раніше ексцентриситету (0,0926 2 = 0,00857). І тоді Кеплер припустив, що орбіта Марса - еліпс, але Сонце розташовується не в його центрі, а в одному з фокусів. Перевірка гіпотези еліпса швидко привела його до успішного завершення роботи, який ознаменував висновком першого закону: Марс рухається по еліпсу, в одному з фокусів якого знаходиться Сонце. Кеплер не сумнівався, що за цим же законом рухаються і інші планети, що незабаром їм було перевірено. Він був упевнений також, що і орбіта Землі - еліпс, але через малу ексцентриситету (e = 0,01673) і недостатньою точності спостережень цей еліпс тоді ще неможливо було відрізнити від окружності. Відкриті Кеплером закони підготували грунт Ньютону для відкриття закону всесвітнього тяжіння.
- константи.Це рівняння є одним з перших трансцендентних рівнянь, які знайшли практичне застосування. Нарешті Кеплер помітив, що бічне стиснення орбіти становить 0,00429 частки радіуса, що точно дорівнює половині квадрата певного ним раніше ексцентриситету (0,0926 2 = 0,00857). І тоді Кеплер припустив, що орбіта Марса - еліпс, але Сонце розташовується не в його центрі, а в одному з фокусів. Перевірка гіпотези еліпса швидко привела його до успішного завершення роботи, який ознаменував висновком першого закону: Марс рухається по еліпсу, в одному з фокусів якого знаходиться Сонце. Кеплер не сумнівався, що за цим же законом рухаються і інші планети, що незабаром їм було перевірено. Він був упевнений також, що і орбіта Землі - еліпс, але через малу ексцентриситету (e = 0,01673) і недостатньою точності спостережень цей еліпс тоді ще неможливо було відрізнити від окружності. Відкриті Кеплером закони підготували грунт Ньютону для відкриття закону всесвітнього тяжіння.