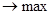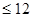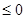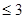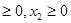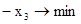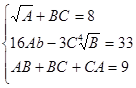Чисельні методи та їх реалізація в Excel
|
Скачати 35.59 Kb.
|
|
| Дата конвертації | 24.02.2020 |
| Розмір | 35.59 Kb. |
| Тип | реферат |
|
|
-
Навігація по даній сторінці:
- Сервіс / Підбір параметра ...
- Значення
- Результат підбору параметра
- Сервіс / Параметри / Обчислення
- Підбором параметра ...
- ТРАНСП
- Готово
- Ctrl / Enter
- Shift / Ctrl / Enter
- додавання матриць
- Транспонування матриці А
- Модель-безліч
- Чисельні методи-методи
- Сервіс / Пошук рішення ... (отримаємо
- умовний екстремум
- Пошук рішення
- Обмеження
- Пошук рішення ...
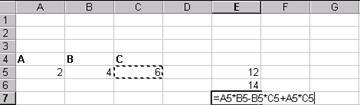
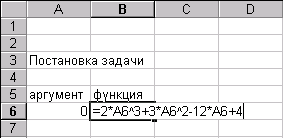
по предмету: '' Моделювання '' на тему: '' Чисельні методи та їх реалізація в Excel '' Виконала: студентка 3-курсу Камчибекова Б. гр. КІС-5-97 Перевірив: к.т.н. професор. Бабак В. Ф. Бішкек - 2000 Глава 1. Підбір параметра ... ... 3 1.1. Нелінійні алгебраїчні рівняння. 3 1.2 Системи двох лінейнихалгебраіческіх рівнянь. 5 Завдання 1. 5 Завдання 2. 5 Глава 2. Матрична алгебра. 6 2.1 Визначник матриці .. 6 2.2 Множення матриць. 7 Завдання 3. 7 Множення на число 14. 9 Завдання 4. 10 2.6 Система лінійних алгебраїчних рівнянь. 14 Завдання 5. 14 Глава3. Пошук рішення ... ... 17 1.2Оптімізація. 17 3.2Безусловний екстремум .. 17 Заданіе6. 18 3.4 Математичне програмування. 22 3.4.1. Лінійне програмування. 23 Завдання 7. 23 Завдання 8. 25 Завдання 9. 25 Завдання 12. 27 Глава 1. Підбір параметра ... 1.1. Нелінійні алгебраїчні рівняння При моделюванні економічних ситуацій часто доводиться вирішувати рівняння виду: f (x, p 1, p 2,..., p n) = 0 (1) де f-задає функція, х-невідома змінна. p 1, p 2,..., p n - параметри моделі. Рішення таких рівнянь може бути як самостійної, так і частиною більш складних завдань. Як правило, дослідника цікавить поведінка рішення в залежності від параметрів p k, k = `1, n Рішеннями або коренями рівняння (1) називають такі значення змінної х, які при підстановці в рівняння звертають його в тотожність. Тільки для лінійних або найпростіших нелінійних рівнянь вдається знайти рішення в аналітичній формі, тобто записати формулу, що виражає шукану величину х в явному вигляді через параметри p k (наприклад формула коренів квадратного рівняння). У більшості ж випадків доводиться вирішувати рівняння (1) чисельними методами, в яких процедура вирішення задається у вигляді багаторазового застосування деякого алгоритму. Отримане рішення завжди є наближеним, хоча може бути як завгодно близько до точного. Розглянемо послідовність дій для отримання рішення нелінійного рівняння в середовищі електронної таблиці. Нехай треба розв'язати рівняння виду:
C формуємо лист електронної таблиці, як показано на рис.1. Рівняння (2) запишемо в клітку С5, починаючи зі знака рівності, а замість змінної x вкажемо адресу клкткі В5, яка містить значення початкового наближення рішення.
замість змінної x вкажемо адресу клітини В5. яка містить значення початкового наближення рішення Метод, застосовуваний в EXCEL для вирішення таких рівнянь модифікований кінцевими різницями метод Ньютона, який дозволяє не сильно дбає про початковому наближенні, як цього вимагають інші чисельні методи рішення рівнянь (метод хорд, дихотомії та ін.) Єдине, що слід врахувати - це те , що буде 'знайдено рішення найближчим до обраного початкового наближення. Для отримання рішення рівняння (2) треба виконати наступну послідовність дій: 1. Виконати команду Сервіс / Підбір параметра ... (отримаємо лист електронної таблиці, як показано на Рис. 2); 2. Заповнити діалогове вікно Підбір параметра ...: 2,1 Клацнути лівою клавішею миші в полі Встановити в осередку, після появи в ньому курсору, перемістити покажчик миші і клацнути на клітці з формулою, в нашому випадку це клітка С5, абсолютний адресу якої $ З $ 5 з'явиться в полі рис.1
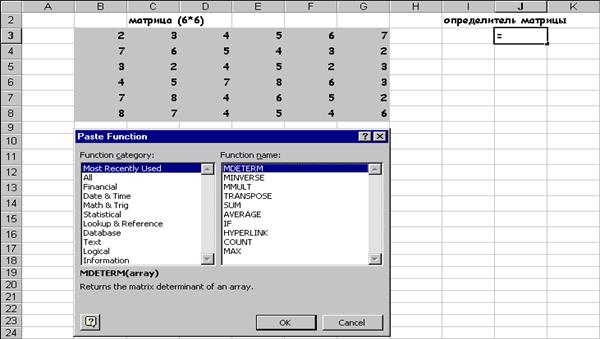
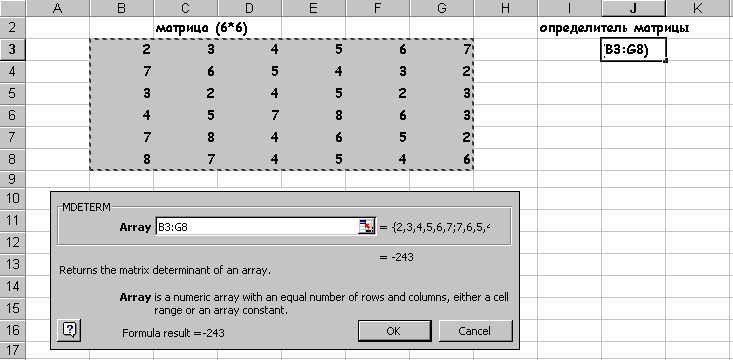
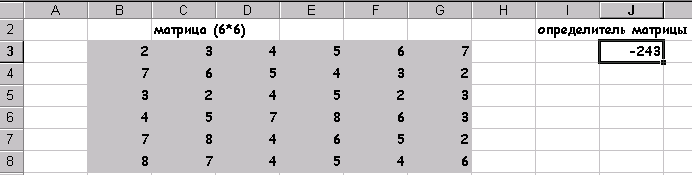
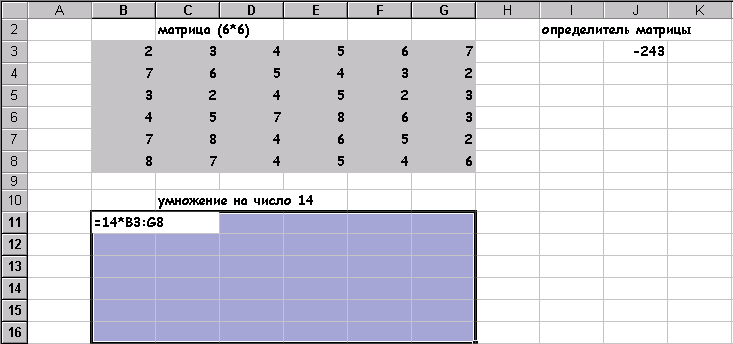
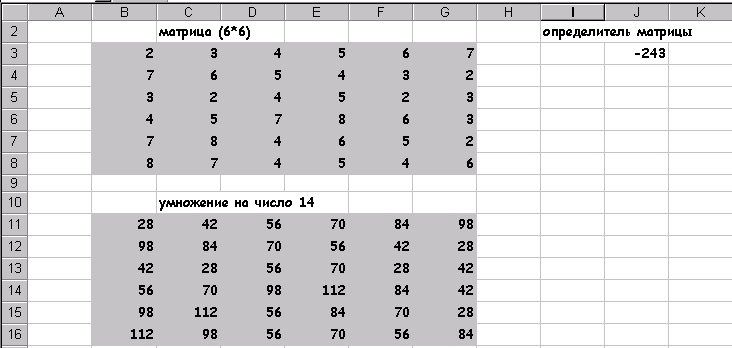
Ця електронна адреса можна було б набрати на клавіатурі, після появи курсору в поле. У ставити в осередку 2.2. У полі Значення ввс У нашому випадку це значення дорівнює О. 2.3 У поле, Змінюючи значення осередки ввести адресу клітини, де задано початкове наближення рішення, в нашому випадку це клітка У 5 (абсолютний адреса якої $ В $ 5 з'явиться в полі після клацання лівої кнопки миші на клітці В5) .Після виконання пунктів 1-2 сторінка електронної таблиці буде виглядати так, як показано на Рис.3. Права частина решаемого рівняння не зобов'язана бути завжди нулем рівняння (2) перетворити до виду 10 * х * (х + 10) / (х-9) = 2. то в поле Значення варто було б встановити 2. Після натискання на кнопці ОК з'явиться вікно Результат підбору параметра, в якому дається про те нацдем чи рішення, чому дорівнює і яка точність отриманого рішення. Для нашого прикладу Результат підбору параметра показаний на Рис.4 При значенні аргументу -0,187204141 функція, що стоїть в лівій частині рівняння (2) відрізняється від нуля на - 0,000484158. Досягнута точність рішення дорівнює - 1.0Е-3 Якщо отримані значення слід "відбити на аркуші електронної таблиці, то треба клацнути на кнопці ОК. .Якщо ж немає то на кнопку Скасування. У першому випадку знайдені значення зафіксуються в клітинах В5 і С5 і лист електронної таблиці буде виглядати як на Рис.5, або як на Рис.6, якщо встановити режим відображення результатів, попередньо знявши режим відображення формул, виконавши команду Сервіс / Параметри / Вид / Формули. Чисельні методи розв'язання рівнянь хороші тим, що м o жно отримати наближене рішення із заданою точністю. EXCEL име (можливість управляти вибором точності. Для цього треба виконай 'команду Сервіс / Параметри / Обчислення та у відповідних повз встановити. Значення відносної похибки і кількості ітераш Рис.7 1.2 Системи двох лінейнихалгебраіческіх рівнянь Вищевикладений спосіб отримання рішення рівняння може бути легко распрастранено для випадку рішення ситеми двох рівнянь з двома невідомими, якщо ситема має такий вигляд. Y = Ф (х) Y = y (х) У кожному рівнянні системи функції у явна виражена через х Перетворимо систему (3) в одне рівняння виду (+) Ф (х) - '^ (х) = 0 - (4) Отримане рівняння вже можна вирішити за допомогою Подбора параметра ... так як це було описано вище. Як приклад розглянемо знаходження рівноважних ціни і обсягу продажів для ринку деякого товару. Нехай функція попиту на товар має вигляд Q = 40 / (Р + 3) а функція пропозиції: Q = 20Р-14 Знайти рівноважні ціну та обсяг, побудувати графіки попиту і пропозиції. Наявну систему рівнянь Q = 40 / (p +3) Q = 20Р-14 перетворимо в одне рівняння виду 40 / (р + 3) - 20 р + 14 = 0 Підбором параметра ... описаним вище, знаходимо рівноважну ціну, вона дорівнює 1,17, підставивши це значення в одне з рівнянь системи, отримаємо і значення рівноважного обсягу - 9,57. Для побудови графіка, ілюструє ситуацію рівноваги попиту та пропозиції на ринку, скористаємося знанням рівноважної ціни і візьмемо значення цін в деякій околиці від неї. наприклад від 0 до 4 з кроком 0,1. Використовуючи всі можливості майстра діаграм, отримаємо наступну ілюстрацію рішення задачі про рівновагу на ринку. Рис.8. Завдання 1 Знайти найближче до початкового наближення рішення наступних рівнянь. Дослідити вплив початкового наближення на знайдене рішення 10 x - x + 56 = 12 завдання 2 Підбором параметра ... знайти точку рівноваги ринку деякого товару, для чого вирішити систему рівнянь, що описують попит і пропозиція цього товару. Побудувати і оформити графік равновес ия. функція попиту Q = 50e-3 функція пропозиції Q = 3p-4e 0 < /p> Глава 2. Матрична алгебра На думку найбільшого економіста нашої епохи В. В. Леонтьєва. «Диференціальне числення і елементарна алгебра - два традиційних інструменту економіста-математика замінюються. або, принаймні доповнюються матричної алгеброю. » 4 Матрична алгебра тісно пов'язана з лінійними функціями і з лінійними обмеженнями у зв'язку з чим знаходить собі застосування в різних економічних завданнях: • в економетрики, для оцінки параметрів множинних лінійних регресій; • при вирішенні задач лінійного програмування; • при макроекономічному моделюванні і т.д. Особливе ставлення до матричної алгебри в економіці з'явилася після створення моделей типу «Витрати - Випуск», де за допомогою матриць технологічних коефіцієнтів пояснюється рівень виробництва в кожній галузі через зв'язок з відповідними рівнями в усіх інших галузях. Електронна таблиця EXCEL має ряд вбудованих функцій для роботи з матрицями: ТРАНСП - транспонування вихідної матриці - обчислення визначника квадратної матриці МОПРЕД - обчислення визначника квадратної матриці МОБР - обчислення матриці зворотного до даної - знаходження матриці, що є твором двох матріц.Кроме того можливе виконання операцій поелементного складання (вирахування) двох матриць і множення (ділення) матриці на число. Всі перераховані вище функції викликаються через майстер функцій і хоча відносяться до розділу математичних, вони розташовуються в повному алфавітному переліку. МУМНОЖ - знаходження матриці, що є твором двох матриць. Крім того можливе виконання операцій поелементного складання (вирахування) двох матриць і множення (ділення) матриці на число. Всі перераховані вище функції викликаються через майстер функцій і хоча відносяться до розділу математичних, вони розташовуються в повному алфавітному переліку. 2.1 Визначник матриці Для обчислення визначника матриці сформуємо лист електронної таблиці, як показано на Рис.9. Місце запису обчисленого визначника матриці визначається місцем розташування табличного курсора. Нехай на аркуші електронної таблиці зроблені всі попередні дії, тобто введена матриця, над якою будуть проводитися дії і визначено місце запису результату. Наступним кроком викликається майстер функцій ріс10., Ліве вікно якого містить перелік розділів, а праве алфавітний список функцій, що становлять даний розділ. У лівому вікні вибираємо розділ - «Повний алфавітний перелік«, а в правому МОПРЕД, У який з'явився діалогом вікні Ріс11. Слід вказати лівий верхній і через двокрапку правий нижній адреси матриці, (або обвести цікаву для нас матрицю, при натиснутоюклавіші миші, штриховий лінією, що автоматизує процес визначення адрес розташування матриці на аркуші ЕТ) Рис.11 Клацнувши на кнопці Готово отримаємо значення визначника, розміщеного в клітці С10. Його значення дорівнює 1 Знаходження визначника - це єдина дія .над матрицею, яка дає в результаті число, інші матричні функції в результаті своїх дій дають матриці і, це, слід, враховувати при підготовці на аркуші ЕТ місця для розміщення результату. 2.2 Множення матриць Як приклад розглянемо множення двох матриць. Нехай треба помножити матрицю А (5 * 4) на матрицю В (4 * 3). це множення можливо, так як число стовпців матриці А збігається з числом рядків матриці В. результатом буде матриця С (5 * 3). Перед викликом функції множення матриць сформуємо лист ЕТ, так як показано на Рис.12 Потім виконаємо наступну послідовність дій: 1.Зададім матрицю А 2. Задамо матрицю В 3 Відзначимо місце для матриці З 7 4. Звернемося до майстра функцій, знайдемо в повному алфавітному переліку функцію МУМНОЖ і виконаємо постановку задачі так. Як показано на Рис. 13 Як масиву 1 вказується діапазон адрес матриці А, а в якості масиву 2 діапаон адрес матриці В. Клацнути в на кнопці Готово отримаємо в клітці, де присутній знак рівності, повний запис функції множення. Для отримання результату необхідно натиснути клавіші Shift / Ctrl / Enter одночасно 8 7 У виділеному під результат місці ЕТ поставити знак рівності. 8 Всі матричні функції, за винятком обчислення визначника. вимагають заключного одночасного натискання клавіш Shift / Ctrl / Enter На Рис 15 показаний результат множення після натискання клав Shift / Ctrl / Enter, а в рядку формул варто вираз в "фігурні дужки, {3 * B 4: D 6} що є ознакою виконання матрично операції додавання матриць Для складання двох матриць однакової розмірності 10 слід виконати наступну послідовність дій. . Задати дві вихідних матриці. . Відзначити місце для матриці - результату. •. У виділеному під результат місці ЕТ поставити знак рівності і записати суму так. як показано на Рис. 16.. -Завершіть виконання роботи натисканням клавіш Shift / Ctrl / Enter, Рис.17 ". Фігурні дужки в рядку формул {В4: D 6 + F 4: H 6} ознака виконання матричної операції завдання 3 Знайти визначник матриці В (6 * 6) :. помножити матрицю на 14.
результат:
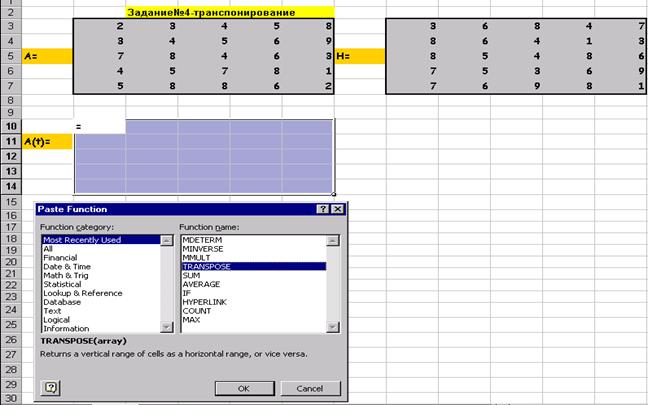
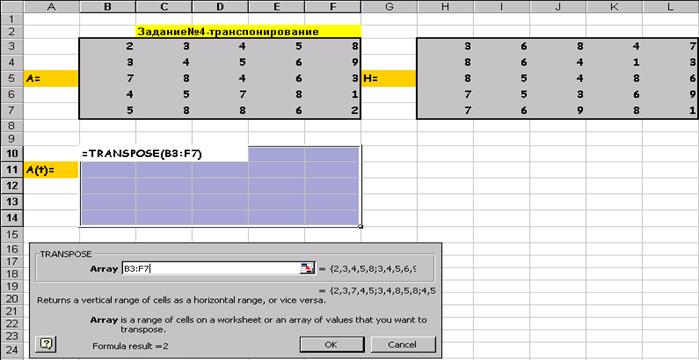
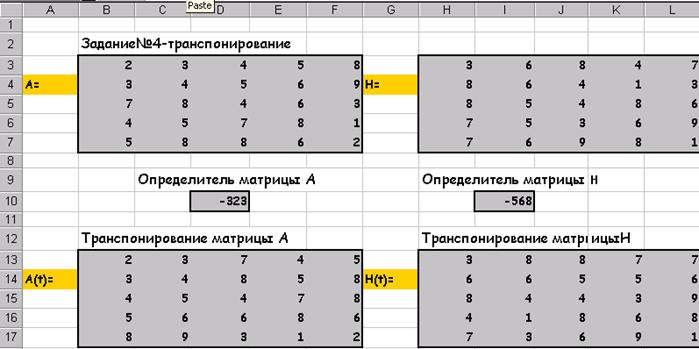
завдання 4 Транспонування матриці А:
Після натискання Shift / Ctrl / Alt:
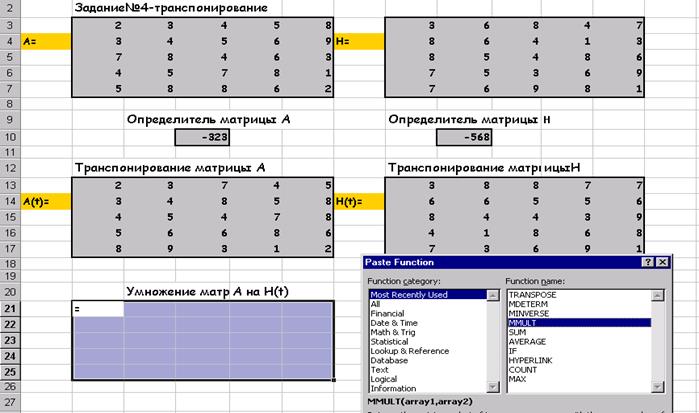
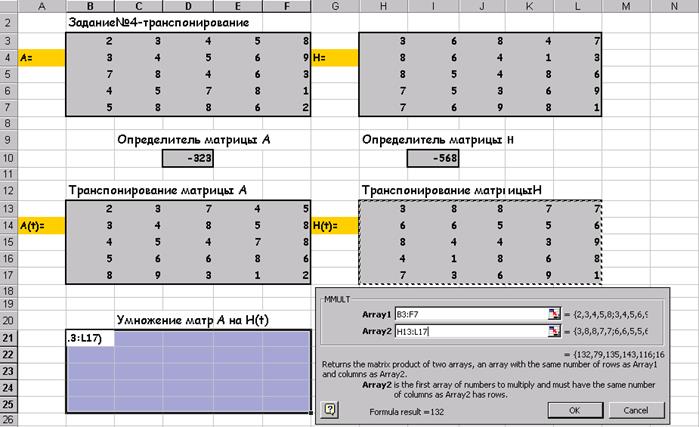
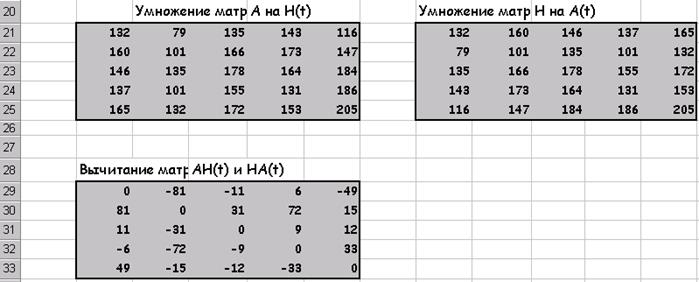
Множення матриць А на H (t):
Після натискання на ОК:
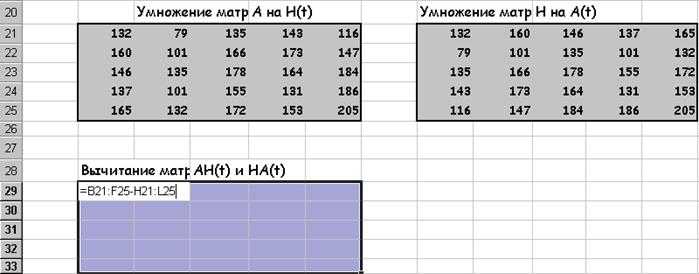
Віднімання матриць AH (t) і HA (t):
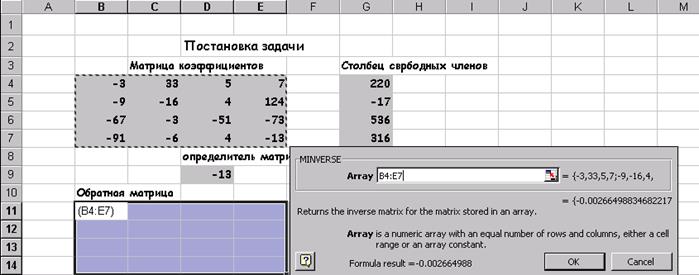
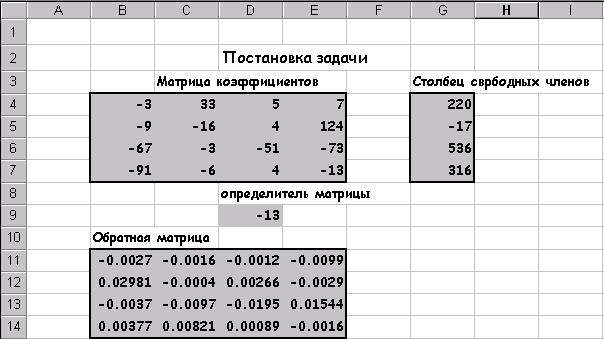
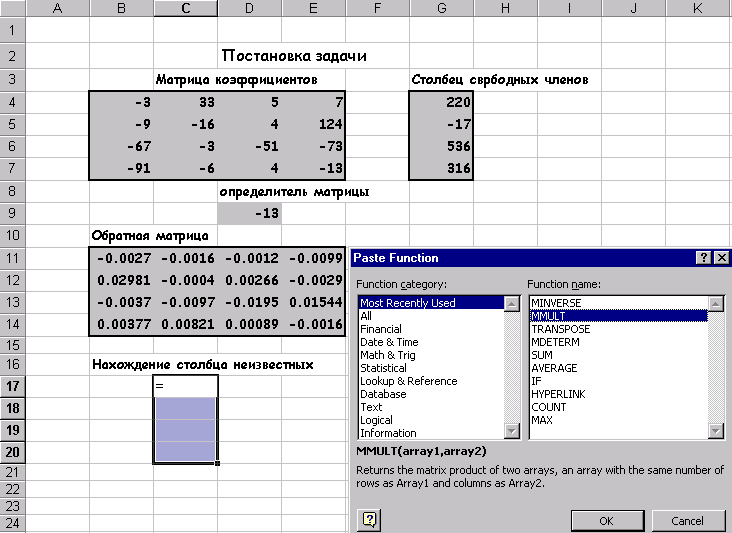
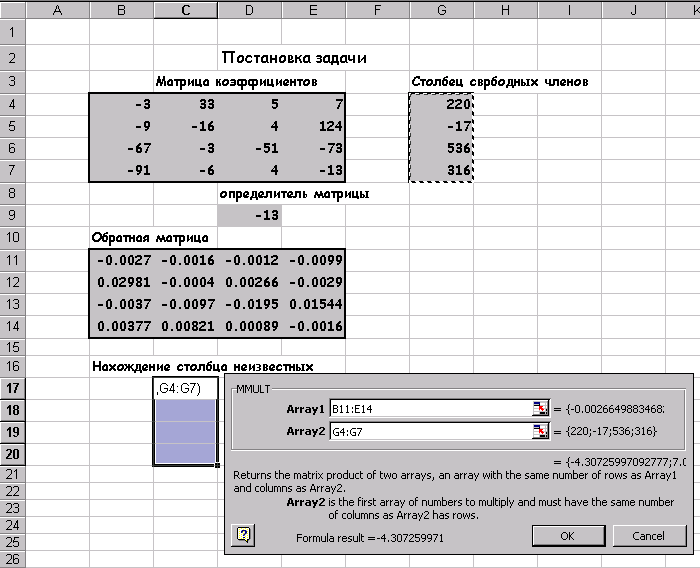
2.6 Система лінійних алгебраїчних рівнянь Рішення Система лінійних алгебраїчних рівнянь завжди займало математиків і для вирішення було розроблено чимало чисельних методів, що підрозділяються на прямі (Гаусса, Кремера) і ітераційні (простих ітерацій, Зейделя, верхніх релакцій ...) EXCEL завдання отримання рішення СЛАР вирішуються за допомогою вищеописаних матричних функцій, для чого вихідну систему треба представити у вигляді матричного рівняння. Розглянемо послідовність дій для отримання рішення СЛАР на конкретному прикладі. завдання 5 Знайти рішення системи лінійних алгебраїчних рівняння і зробити перевірку.
Для того, щоб система (5) мала єдине рішення необхідно і досить, щоб визначити системи, складений з коефіцієнтів при змінних х, х, х, х, що не дорівнював нулю. Розрахуємо визначити системи користуючись функцією МОПРЕД. Розраховане значення визначника системи дорівнює 1662723продолжать процес пошуку рішення. З лінійної алгебри відома матрична запис системи рівнянь і матричне кончина рішення. Перепишемо систему рівнянь (5): Тоді матричний рішення рівняння виглядає так: Результат, вказаний на ріс18 можна отримати, виконавши такі дії: 1. Обчислити визначник і з'ясувати чи має система єдине рішення. 2. Обчислити матрицю зворотну до вихідної. 3. Знайти добуток зворотної матриці і вектор стовпця вільних членів. Глава3. Пошук рішення… 1.2Оптімізація Майже будь-яку ситуацію, котра трапляється нам в діловій особистої суспільного життя можна охарактеризувати як ситуацію прийняття рішення. Для задач прийняття рішень істотними є наступні загальні елементи: 1. Безліч змінних і параметрів. В їх число входять: Безліч дозволяють або ендогенних змінних, значення яких розраховуються особою, яка приймає рішення. Безліч зовнішніх або екзогенних змінних, значення яких не контролюються особою, яка приймає рішення. Безліч параметрів, які так само контролюється і вважаються в умовах завдання цілком визначеними. Модель-безліч співвідношень, що зв'язують всі змінні і параметри. Цільова функція-функція, функцій, значення якої залежить від значень ендогенних змінних. Ця функція. Дозволяє особі, що приймає рішення оцінювати варіанти. Чисельні методи-методи, за допомогою, яких можна систематично оцінювати результати різних рішень. Отримання рішення на моделі, в кінцевому підсумку, зводиться до математичної задачі знаходження деяких речових значень ендогенних змінних, які оптимізують цільову функцію. Якщо до недавнього часу всі чотири перераховані вище елемента лягали на обличчя приймає рішення, то тепер уміння користуватися вбудованими функціями EXCEL знімає найбільш виснажливий пункт, а саме, застосування чисельних методів, і робить дослідження задач прийняття рішення більш ефективними, так як тепер для вирішення однієї і тієї ж більш ефективними, так як тепер для вирішення однієї і тієї ж задачі можна швидко переглянути різного виду постановки в тому числі і відрізняються один від одного по структурі. 3.2Безусловний екстремум Excel володіє потужним вбудованим засобом для знаходження екстремальних значень функції однієї або кількох змінних. Для одно-екстремальних функцій можна знайти безумовний глобальний екстремум. Для багатоекстремального функцій можна знайти умовний локальний екстремум. Забігаючи наперед відзначимо, що для багатоекстремального функцій визначити, який із локальних екстремумів буде знайдений неможливо без побудови графіка функції на який нас цікавить інтервалі, так як чисельні методи знаходження екстремуму орієнтовані на пошук найближчого рішення до точки початкового наближення і взагалі кажучи, вимагають унімодальне функції. Подивимося різні приклади пошуку екстремальних значень функції. Заданіе6 Знайти мінімум і максимум функції на інтервалі, побудувати графік. 2.
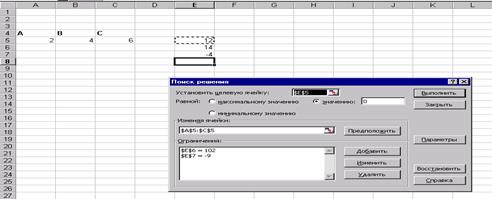
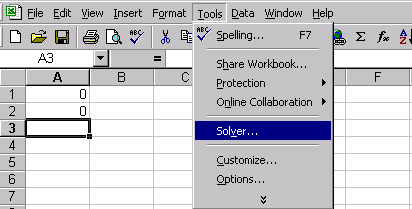
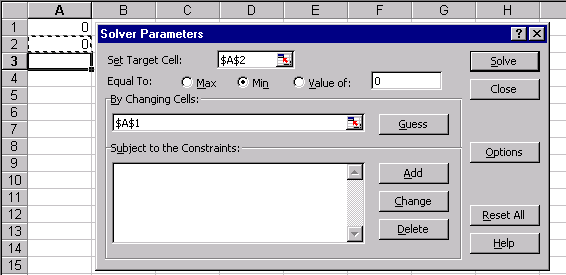
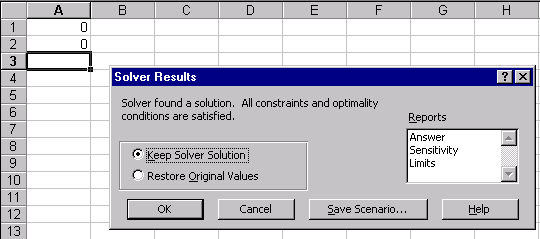
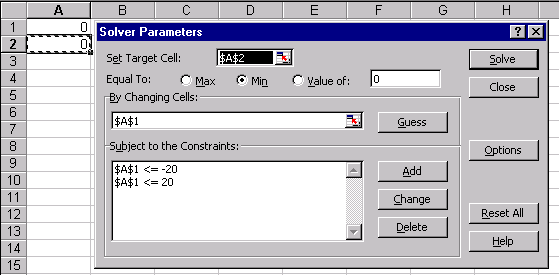
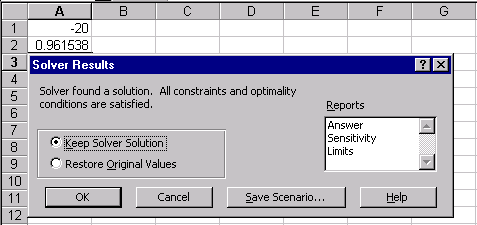
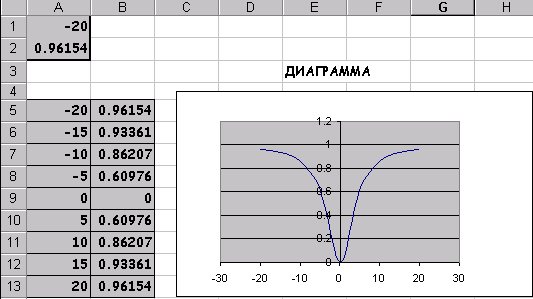
Рис.19 Для пошуку безумовного екстремуму функції сформуємо лист електронної таблиці, як показано на малюнку 20. Функцію (6) запишемо в клітку А2 де замість змінної х слід вказати адресу комірки А1, яка містить початкове наближення екстремуму рівне, наприклад 0. Для пошуку мінімуму слід виконати наступну послідовність дій: 1.Виполніте команду Сервіс / Пошук рішення ... (отримаємо лист електронної таблиці, як показано на рис.20). 2.Заполніть діалогове вікно Пошук рішення ... ріс21 2.1.Щелкнуть лівою клавішею миші в поле. У ставити цільову комірку і клацнути на осередку з формулою, в нашому випадку це осередок А2, абсолютний адреса якої. $ А $ 2 з'явиться в поле. 2.2. Вибрати поле Мінімальне значення. 2.3. В полі. І Редагувати осередку ввести адреси осередків, значення яких будуть варіюватися в процесі пошуку рішення. У нашому випадку це клеікаА1, абсолютний адреса якої. $ А $ 1. Після виконання пунктів 1-2 лист електронної таблиці буде виглядати так, як показано на рис 21. Після клацання на кнопці Виконати отримаємо рішення поставленого завдання. У клітці А1 знаходиться значення змінної Х рівне 0.769231 при якому функція (5) досягає мінімального значення рівного -167,692. Ріс22 умовний екстремум Для функції однієї змінної пошук екстремуму можливий як на всій числовій осі, так і на деякому інтервалі, пошук на інтервалі вже можна вважати пошуком умовного екстремуму функції, т.к з'являються обмеження на зміну значень аргументу. На рис.21 в діалогом вікні Пошук рішення є поле Обмеження м відповідні йому команди: Додати, Замінити, Видалити. Розглянемо попередню задачу, додавши умова пошуку мінімального значення на інтервалі [1; 5]. Тоді діалогове вікно Пошук рішення ... слід видозмінити, додавши обмеження: Клацнувши лівою клавішею миші в полі Обмеження і потім на кнопці Додати, відкриємо діалогове вікно Додавання обмеження. Ріс23 ,,, .. яке слід заповнити так як показано на малюнку. Після додавання останнього обмеження діалогове вікно Пошук рішення ... буде містити математичну постановку задачі екстремуму і виглядає след.образом. У = -167 при х = 1, яке відрізняється від рішення, отриманого в попередньому випадку. Тут в якості мінімального значення виступає найменше значення функції на інтервалі [1; 5], що збігається з лівого кордоном інтервалу. Всі чисельні методи знаходження оптимальних значень для коректної роботи вимагають, щоб функція на інтервалі була унімодальної. При такій постановці завдання значення праці і капіталу визначається як 5 і 2 одиниці відповідно. Отримувані значення цільової функції при цьому одно 3.37. Тепер можна побудувати графік, на якому відображені лінія байдужості використання праці і капіталу при випуску 3.37 і лінія обмеження на кошти, призначені для витрат на працю і капітал. Отримані криві стосуються в знайденої точці, що узгоджується з теорією фірми. рис 31
3.4 Математичне програмування Різні методи оптимального управління, які отримали помітний розвиток в другій половині двадцятого століття, завдяки створенню та поширенню комп'ютерної техніки, не тільки відповідають нагальним потребам економічної науки, а й починають грати роль найважливішого її складового елементу. І це цілком природно, оскільки одним із головних завдань економічної науки є розробка теоретичного фундаменту управління, тобто методів найкращого розподілу обмежених ресурсів (людських, матеріально -вещественних, фінансових, часових) для підтримки функціонування і розвитку підприємства або економіки країни. Однак, щоб виявити глибинний зв'язок між математичним програмуванням і економічною наукою, знадобилися зусилля багатьох вчених. Аналізуючи можливості Пошуку рішення ... можна помітити, що він застосовний для вирішення досить широкого класу задач математичного програмування. Якщо завдання прийняття рішень в галузі управління можна сформулювати у вигляді підлеглих m довільним обмеженням.
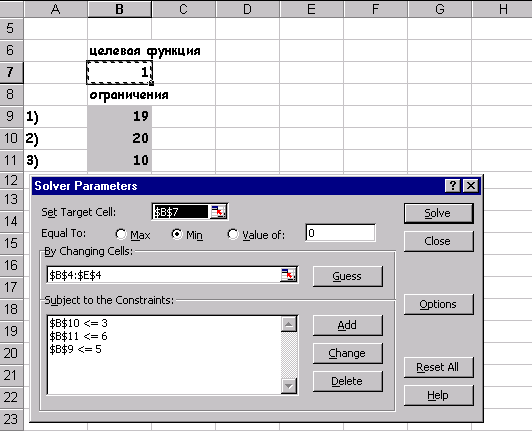
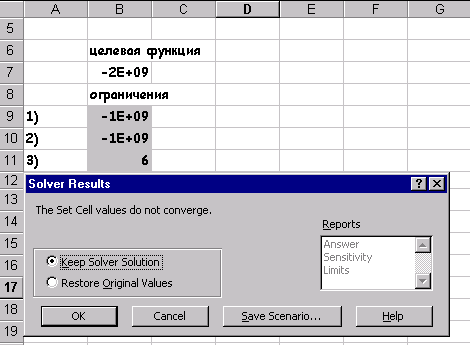
........................ g m (x 1, x 2,..., x n) то Пошук рішення ... дозволяє знайти рішення такого завдання, яка в формальної постановки може бути завданням: 1. лінійного програмування 2. нелінійного програмування 3. цілочисельного програмування 4. частково цілочисельного програмування Крім того у осіб, що приймає рішення є можливість змінити параметри роботи Пошуку рішення ..., що підвищують ефективність пошуку оптимального рішення. рис.32 3.4.1. лінійне програмування
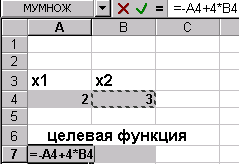
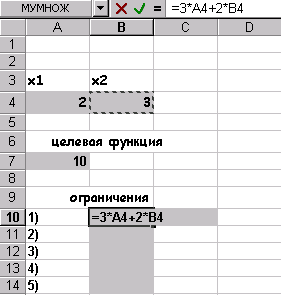
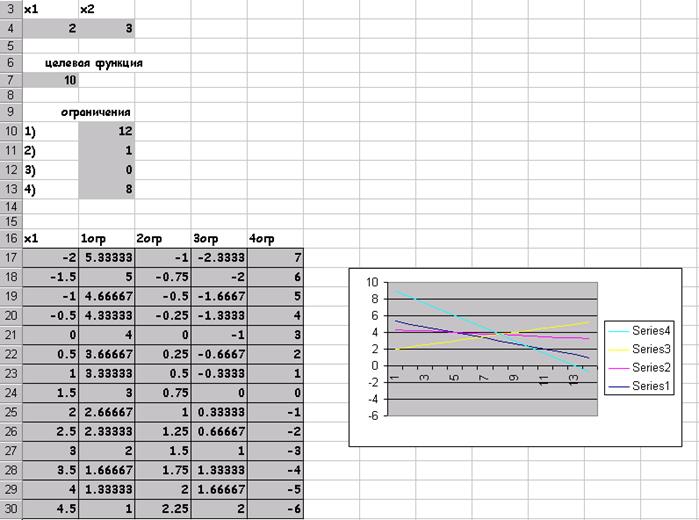
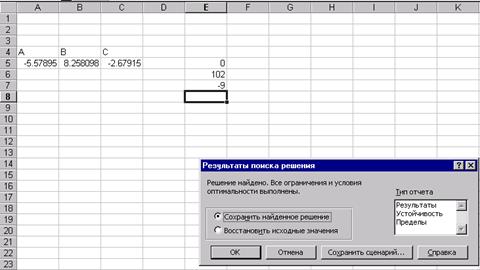
Сформуємо сторінку електронної таблиці і постановку задачі лінійного програмування в діалоговому вікні Пошуку рішення ... Після виконання поставленого завдання отримуємо таке значення змінних Як бачимо, при знайдених значеннях x 1, x 2 цільова функція приймає мінімальне значення, рівне -9.66 і цим задовольняються всі обмеження поставленого завдання. Графічне рішення поставленого завдання виглядає так: завдання 7 Вирішити задачу лінійного програмування за допомогою Пошуку рішення ..., показати графічно область допустимих рішень і цільову функцію. 2.F = -x 1 + 4x 2 при 3 x 1 +2 x 2 2 x 1 - x 2 -3 x 1 +2 x 2 x 1 +2 x 2 x 1
завдання 8 За описом завдання зробити математичну постановку, решіть.создать звіт і прокоментувати його. №2 Фірма виготовляє два типи електричних вимикачів, типу А, дохід від яких дорівнює 0.4 $. На кожен вимикач і типу В - дохід від яких дорівнює 0.3 $. На виготовлення вимикача А потрібно в три рази більше робочого часу, ніж на виготовлення типу В. Якби виготовлялися вимикачі тільки типу В, то денного робочого часу вистачило б для виготовлення рівно 1000 вимикачів. Поставка мідного дроту забезпечує виготовлення тільки 800 вимикачів в день (будь-якого типу). Для вимикачів потрібні спеціальні ізолятори, їх можна отримати в день для типу А не більше 400, для типу В не більше 700. Завдання полягає в максимізації доходу при всіх зазначених вище обмеження. завдання 9 Скласти задачу двоїсту до даної задачі лінійного програмування і вирішити обидві за допомогою Пошуку рішення ... 2.F = -x 1 + x 2 при x 1 +2 x 2 - x 3 £ 5 2 x 2 + x 4 £ 3 x 3 +2 x 4 £ 6 x j ³ 0.j = 1.4
завдання 12 За допомогою Пошуку рішення ... знайти рішення системи нелінійних алгебраїчних рівнянь.Дослідити залежність одержуваного рішення від різних початкових наближень (менше трьох), оформити дослідження у вигляді таблиці. №2
ЛІТЕРАТУРА: 1. EXCEL 5.0 Для професіоналів. М-1995 2. EXCEL7.0 М-1997 3. А.А.Горчаков, І.В.Орлов. Комп'ютерні економіко-математичні моделі. М-1995 4. І.Л.Акуліч. Математичне програмування а в прикладах і задачах. М -1986 5. М.Кубоніва. Математична економіка на персональному комп'ютері. М-1991. |
- Сервіс / Підбір параметра ...
- Значення
- Результат підбору параметра
- Сервіс / Параметри / Обчислення
- Підбором параметра ...
- ТРАНСП
- Готово
- Ctrl / Enter
- Shift / Ctrl / Enter
- додавання матриць
- Транспонування матриці А
- Модель-безліч
- Чисельні методи-методи
- Сервіс / Пошук рішення ... (отримаємо
- умовний екстремум
- Пошук рішення
- Обмеження
- Пошук рішення ...

 (2)
(2)

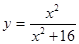


 при
при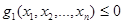
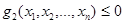
 0
0 Знайти мінімум функції F = 5 x 1 + x 2
Знайти мінімум функції F = 5 x 1 + x 2  min
min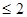
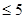
 x 1, x 2 - довільні
x 1, x 2 - довільні