Історичні проблеми фізики. Сила, маса, інерціальна система відліку
|
Скачати 74.38 Kb.
|
|
| Дата конвертації | 03.04.2019 |
| Розмір | 74.38 Kb. |
| Тип | стаття |
|
|
-
Навігація по даній сторінці:
- Система відліку
- Випадок великих швидкостей
- Список літератури
|
. А.І. Сомсіков Визначення сили і маси У фізиці сенс кожної знову вводиться величини, крім початкових, вважається з'ясованим в тому випадку, коли знайдено рівняння, в якому ця величина виражається через раніше введені, початкові ж величини не виводяться. Наприклад, швидкість визначається як відношення пройденого шляху до часу, протягом якого шлях пройдено (шлях і час - початкові поняття, що не піддаються подальшому розкладанню); прискорення є відношення величини зміни швидкості до часу, протягом якого відбулася зміна; робота є твір сили на пройдений шлях; потужність є відношення роботи до проміжку часу, протягом якого вона відбувалася і т.д. Не всі величини, однак, мають настільки ясно певний фізичний зміст і, перш за все, дві фундаментальні величини класичної механіки - сила і маса. Причина полягає в тому, що Ньютон ввів одночасно обидві ці величини в одному рівнянні другого закону механіки, внаслідок чого одна невідома величина - сила визначалася через іншу невідому - масу і навпаки. Логічне коло може бути подолана шляхом додавання другого рівняння, що містить ті ж невідомі, вилучення одного з невідомих і вирази другий невідомої через відомі. Відсутня рівняння було також дано Ньютоном (закон всесвітнього тяжіння для нерухомих і повільно рухаються щодо швидкості світла тел), так що повна система двох рівнянь є:
Для того щоб з'ясувати фізичний зміст вхідних величин Отже, нехай сила, що викликає прискорене рух тіла з масою
після скорочення Звідки: поклавши тепер Масою тіла називається твір прискорення, що купується іншим тілом, що знаходиться на заданій відстані від нього, на квадрат відстані між тілами. З формули видно, що можливо як скалярний, так і векторний тлумачення маси:
Другий закон механіки є феноменологічним визначенням сили (якщо покласти
Сила є твір прискорень взаємодіючих тіл на квадрат відстані між тілами. З визначення випливає, що правильно говорити "сила тел" замість "сила, прикладена до тіла", тому що сила не є самостійною сутністю, що може бути доданою, але лише зазначеним вище твором. Повна система рівнянь ньютоновой динаміки складається з 4-х рівнянь:
і містить 4 невідомих - Вирішення цієї системи є:
Зауважимо, що відсутність або зміна будь-якого з наведених рівнянь робить в першому випадку неможливим однозначне визначення сили і маси, тому що при цьому залишається 3 рівняння з 4-ма невідомими, а в другому рівносильно повної зміни сенсу А тому, якщо де-небудь рівність Система відліку Система відліку СО, в якій вимірюються прискорення Основною властивістю ІСО є незалежність прискорення тіла 1 від самого цього тіла (сталість маси тіла 2 при зміні тіла 1), точно так же прискорення тіла 2 не залежить від самого тіла 2 (сталість маси тіла 1 при зміні тіла 2). Це означає, що в ІСО приріст прискорення зі зміною тіла 1 відноситься кожен раз до тіла 2, відповідно зі зміною тіла 2 вважається такою, що до тіла 1. Іншими словами, зі зміною тіла 1 прискорення системи відліку щодо тіла 1 не змінюється (система відліку залишається колишньою), точно так же зі зміною тіла 2 прискорення системи відліку щодо тіла 2 не змінюється. Звідси випливає, що для будь-якої пари 1 ', 2' ІСО залишається тією ж самою, що і для 1, 2. Справді, довільну пару 1 ', 2' можна отримати із заданої пари 1, 2 шляхом послідовної заміни спочатку тіла 1 на тіло 1 ', при цьому відносно 1' ІСО рухається з колишнім прискоренням У підсумку, прискорення тел 1 ', 2' вимірюються щодо тієї ж системи відліку, що і прискорення тел 1, 2, з точністю до будь-якої іншої системи, що рухається відносно першої без прискорення. В ІСО прискорення тіла 1 і пов'язаної з ним системи відліку СО1 одно У СО1 прискорення ІСО одно мінус Приєднаємо до тіла 1 деяке тіло 3. При цьому прискорення СО2 в ІСО стає рівним У СО1 прискорення СО2 стає рівним Таким чином, приріст Але це збільшення в ІСО однозначно визначає масу тіла 3! Зауважимо, що як тільки знайдена маса хоча б одного з тіл (в даному випадку - тіла 3), маси всіх інших тіл знаходяться легко, для чого слід послідовно поміщати досліджувані тіла на заданому відстані від тіла 3 і вимірювати прискорення досліджуваних тел щодо тіла 3. При цьому отримаємо: де
Звідки:
де Вищесказане є аналізом історично даного матеріалу. Правильний порядок побудови феноменологічної теорії динаміки наступний. початок побудови Геометричне порівняння тел здійснюється шляхом порівняння їх розмірів; у фізиці тіла порівнюють по їх рухам, Дослідним шляхом встановлено, що тіла, що можуть вільно переміщатися один щодо одного, мимовільно починають рухатися (взаємодіють), причому в системі відліку, пов'язаної з тілом 1 (СО1) тіло 2 набуває прискорення Однак це прискорення ще не може служити характеристикою тіла 1 перш за все тому, що це величина неоднозначна, а залежить ще і від відстані: Величиною, що не залежить від відстані, є твір: Однак і ця величина ще не може служити характеристикою тіла 1, тому що вона залежить не тільки від тіла 1, але і від тіла 2, іншими словами зі зміною тіла 2 прискорення
Зробити це прискорення не залежних від тіла 2 можна шляхом переходу до іншої системи відліку (названої інерціальній СО або ІСО), що рухається прискорено щодо СО1 (самого тіла 1) з деяким прискоренням Знайти ІСО значить визначити Нехай дано тіло 1 спільно з його системою відліку СО1 і тіло 2. У СО1 прискорення тіла 2 одно У шуканої ІСО прискорення тел 1, 2 складають: При цьому: Нерухомо приєднаємо до тіла 1 деяке тіло 3. У шуканої ІСО спільне прискорення тел (1 + 3) не залежить від тіла 1 і складає, як і раніше Прискорення тіла 2 рівні тепер: в ІСО - При цьому: нехай: маємо: Приберемо тепер тіло 1. У шуканої ІСО прискорення що залишився тіла 3 не зміниться і складає, як і раніше Прискорення тіла 2 рівні тепер: в ІСО - При цьому: обидва прискорення
знаючи
знаючи
при заданому У свою чергу твір Ця характеристика отримала найменування маси:
Вибір ІСО, не пов'язаної ні з одним з взаємодіючих тіл, що рухається прискорено щодо кожного з тіл і до того ж з різними прискореннями пояснюється саме тим, що при цьому досягається однозначність характеристик кожного з взаємодіючих тіл. коефіцієнти Вихідні формули при побудові систем одиниць динаміки Ньютона наступні:
В системі одиниць, запропонованої В. Томпсоном, обидва коефіцієнта
при цьому сам еталон маси виявляється цілком певним (~ 15 т, при одиниці довжини - див і одиниці часу - с). Покажемо, як з'являються коефіцієнти у формулах Ньютона у випадку, якщо еталон маси вибирається довільно. Нехай, наприклад, новий еталон маси становить тоді: В системі одиниць типу "динамічної"
оскільки: то отримуємо: В системі одиниць типу "гравітаційної"
Другий закон Ньютона:
В окремому випадку, коли коефіцієнт в точності дорівнює "гравітаційної постійної", ми отримуємо власне гравітаційну і власне динамічну системи одиниць. Якщо новий еталон маси, вимірюваний в частках від томсонова еталона маси, зберігає колишню розмірність [см3 / c2], то коефіцієнт є число, що показує у скільки разів новий еталон більше або менше томсонова еталона. Якщо ж новому стандарту дано і нову назву (наприклад, грам), то коефіцієнт набуває розмірність:
Отже, гравітаційна і динамічна постійні з'являються внаслідок довільності вибору еталона маси при побудові систем одиниць вимірювання і не мають власного фізичного сенсу. Випадок великих швидкостей Якщо вважати встановленим існування граничної відносної швидкості переміщення взаємодіючих тіл, при наближенні до якої їх прискорення прагнуть до нуля за формулами:
де
Взагалі кажучи, Математично обидва варіанти рівноцінні. Однак фізично Тому ми і говоримо, що Крім того, оскільки
При наближенні до граничної швидкості Маса одного і того ж тіла дорівнює нулю для тіл, які досягли граничної відносної швидкості визначення заряду Закон Кулона: За визначенням: взаємодіючими тілами (в ІСО). Звідки: поклавши тепер
іншими словами поняття "заряду" тотожне поняттю маси. Далі: F = a1 a2 r2 = a1 q1 = a2q2, - другий закон Ньютона в області електростатики. За визначенням, напруженість електростатичного поля Векторне тлумачення заряду: потенційність поля Якщо в напрямку дії поля пробне тіло рухається з граничною відносною швидкістю Якщо в зворотному напрямку той же шлях проходиться з відносною швидкістю меншою граничної, то тоді Сумарна робота по замкнутому шляху виявляється не дорівнює нулю. Потенційність поля, що встановлюється за ознакою рівності нулю роботи при переміщенні пробного тіла по замкнутому шляху, порушується в загальному випадку, що включає граничну відносну швидкість Перехід від ІСО до СО1 Перенесемо тепер тіло 2 з СО2 в СО1, нерухомо приєднавши його до тіла 1. В ІСО до перенесення тіла 2: У СО1 до перенесення тіла 2:
В ІСО після перенесення тіла 2:
При цьому У СО1 після перенесення тіла 2:
оскільки
Тому перехід від ІСО до СО1 рівнозначний переносу в цю СО1 тіла 2, що супроводжується підсумовуванням мас І назад, перехід від СО1 до ІСО рівнозначний виділенню з тіла 1, що знаходиться в СО1, деякого тіла 2 з масою Після перенесення тіла 2 в СО1 спільна маса тіл, що знаходяться в СО1: Отже, для тіла, що знаходиться в СО1, маса тіла може бути знайдена вимірами в самій СО1, при використанні в процесі вимірювань тіла нескінченно малої (не обурюються) маси Взаємодія тіл з суттєво різними масами В окремому випадку взаємодії маса тіла 2 може бути багато менше маси тіла 1: Виконаємо перехід від ІСО до СО1 для даного випадку. В ІСО до переходу до СО1 (перенесення тіла 2 в СО1):
У СО1 до перенесення тіла 2:
зважаючи на крихту
В ІСО після переходу до СО1, відповідного переносу в СО1 тіла 2 з масою зважаючи на крихту У СО1 після перенесення в неї тіла 2: тобто приєднання тіла 2 малої маси експеримент Галілея Саме такий випадок виявлений в експерименті Галілея, "спростували" теза Аристотеля про нерівність прискорень тіл, що володіють різними масами. Експеримент, виконаний в СО1, де тіло 1 - Земля (об'єкт з дуже великою масою Справді, при Отже, результат Галілея відноситься до окремого випадку взаємодії тіл з суттєво нерівними масами. Він встановлює фактично спосіб визначення СО1 як місцевої ІСО щодо деяких, цілком визначених для даної СО1 і даної точності вимірювань галілеївських об'єктів за допомогою самих цих об'єктів. Його висновок такий: "Даний експеримент встановлює, що для даних галілеївських об'єктів дане небесне тіло є тілом досить великої маси Для тіла 1 з малою масою Подивимося тепер, як виглядає експеримент Галілея в загальному випадку, спочатку для довільної маси Визначимо попередньо необхідні умови проведення експерименту. Нехай ми бажаємо спостерігати падіння тіла 2 'великої маси в два рази швидше падіння тіла 2 "галилеевской маси. Це означає, що за час проходження тілом 2 'шляху Тому в СО1, де тіло 1 - Земля (об'єкт багато більшої маси Оскільки прискорення будь-якого тіла 2 в СО1 одно:
то маємо: для галилеевского об'єкта Для шуканого об'єкта великої маси
але отже Таким чином з'ясовується, що шуканий об'єкт 2 'великої маси Тому отримане Галілеєм рівність прискорень є всього лише результат "вдало" обраних галілеївських об'єктів. Оцінимо порядок величин, які намагався виявити Галілей. нехай випередження
де при
Звідки Якщо тепер вибрати в якості тіла 1 тіло пренебрежимо малої маси Для цього достатньо забезпечити при масі дробинки При цьому, однак, виникає нова трудність: при При такому прискоренні
тобто уявний Галілей не доживе до кінця експерименту, а за час життя реального Галілея
так що необхідна точність вимірювань Якщо вважати, що така точність вимірювань не досяжна на практиці, то тим більше недосяжна точність вимірювання за програмою "Галілей" за час спостереження
При цьому експериментатор ризикує знову прийти до невірного висновку: "прискорення тіл не залежить від їх маси" і навіть в збільшеному вигляді "переміщення тіл не залежать від маси". Отже, положення Аристотеля відноситься до іншого окремого випадку зворотного співвідношення мас Фактично результат Аристотеля реалізується в самому експерименті Галілея при переході від СО1 до СО2, що утворює свого роду "інверсію" точки зору. Таким чином, обидва положення: Аристотеля - "прискорення тіла пропорційно масі тіла" і Галілея - "прискорення тіла не залежить від маси тіла" дійсно відносяться до одного і того ж окремого випадку взаємодії тіл 1, 2 з істотно нерівними масами. При цьому, однак, для Обидва "взаємовиключні" положення виявляються вірними, відносяться до одного і того ж окремого випадку взаємодії і "підтверджуються" одним і тим же експериментом, але тільки лише в різних СО. У загальному ж випадку вірним є положення Ньютона: "В ІСО, для даної пари 1, 2, прискорення об'єкта 2 не залежить від його маси випадок Ньютона Нехай тепер обидва тіла 1 і 2 мають не галілеївські великі маси. Назвемо їх ньютоновскими об'єктами
де нехай, як і раніше тоді оскільки З урахуванням: При деякому порядку малості, що визначається заданою точністю вимірів, обидва прискорення досягають значень, прийнятих за нульові, причому
Оскільки при цьому Отже, при взаємодії ньютоновского і галилеевского об'єктів
при будь-якому При взаємодії двох ньютоновских об'єктів
тобто визначимо тепер нехай В ІСО прискорення тел 1, 2 складають:
Видно що якщо тепер При цьому: оскільки Звідки мінімальне ньютонівської відстань Наприклад, в ньютонівської системі 1, 2, де тіло 1 - Земля,
Приймемо тепер СО1 як наближеною ІСО. отримаємо: При цьому похибка наближення становить:
При заданій похибки наближення, наприклад,
оскільки реальне При меншому дозволяється за значенні похибки наближення, наприклад, Ньютоновский питання, зазвичай виражається приблизно так: "Чи є сила, що діє на відстані до Місяця, силою того ж роду, що і на поверхні Землі" або, в кілька уточненої формулюванні: "Чи є сила, що діє на ньютоновский" великий "об'єкт, що знаходиться на відстані до Місяця, силою того ж роду, що і діюча на галилеевский "малий" об'єкт, що знаходиться, взагалі кажучи, на будь-якій відстані, в тому числі і на відстані до Місяця ", в формі якнайкраще відповідає суті пошуків Ньютона, може виглядати ще й так: "чи є СО двох ньютоновских "великих" об'єктів, що знаходяться на ньютонівських "великих" відстанях один від одного, тієї ж самої, що і ІСО ньютоновского і галилеевского об'єктів, для яких Відповідь така: "Так, якщо маса одного ньютоновского об'єкта багато більше маси іншого
тобто досить велике, щоб, в межах точності обчислень, яка визначається допускаються похибками З зазначеної вище точністю саме такий випадок має місце в ньютонівських околицях Землі, що і дозволило самому Ньютону зрозуміти ту обставину, що взаємодія тел простягається на ньютонівські відстані. Слід, однак, пам'ятати і інші можливі варіанти відповіді: "Ні, якщо обидва ньютоновских об'єкта близькі один одному по масі "Ні, якщо маси ньютоновских об'єктів задовольняють умові
При наявності в ньютонівських околицях тіла 1 з масою Якщо при цьому тіло 1 маємо масу При цьому СО1 є спільною наближеною ІСО системи, утвореної система Коперника Саме такий випадок виявлений в масштабі сонячної системи, де тіло 1 - Сонце, що і зафіксовано в геліоцентричної системи опису рухів небесних тіл. Відкриття Коперника, до сих пір виражається в логічно суперечливою формі: "Планети обертаються навколо Сонця" (оскільки рух щодо і визначається обраної СО), в світлі законів Ньютона виглядає інакше: "Сонце є ньютоновским об'єктом, маса Дійсно, для пари Сонце - Меркурій,
Для пари Сонце - Земля, де Для трьох зазначених пар прийняття СО1 як наближеною місцевої ІСО супроводжується абсолютною похибкою При цьому відносна похибка Однак як би не була мала вихідна похибка наближення, відповідна їй накопичена похибка, наприклад, при розрахунку поточного просторового положення ньютоновских об'єктів визначається тривалістю спостереження і через певний проміжок часу перевищить похибка визначення фактичного положення, що і виявиться у вигляді невідповідності розрахункового положення. Тому справжня ІСО все ж не є СО1 і всі планети зовсім не "обертаються навколо Сонця", а разом з ним - навколо загального центру мас сонячної системи, як раз і утворює справжню ІСО. А як це викладається в підручниках фізики? В роботі [1] виявлено помилковість розуміння першого закону Ньютона (закону інерції), що визначає траєкторію інерційних рухів. Подивимося тепер, як фізика розуміє ІСО. Наведемо лише один приклад, що відображає це розуміння. Цитата: "З визначення механічного руху як простого переміщення випливає, що це переміщення може відбуватися лише щодо будь-яких інших матеріальних тел. Тому для того, щоб отримати можливість характеризувати рух будь-якого тіла, перш за все слід домовитися, щодо якого іншого тіла (або групи нерухомих одна відносно іншої тел) ми будемо відраховувати переміщення даного тіла. Це тіло (або група тіл) утворює систему відліку. Таким чином, кожен рух має розглядатися щодо будь-якої певної системи відліку. У різних випадках система відліку може вибиратися різним чином, але виразно характеризувати дане рух ми можемо, тільки твердо вибравши систему відліку. Наприклад, кинувши який-небудь предмет, ми можемо розглядати його рух щодо кімнати; в цьому випадку систему відліку утворюють стіни, підлогу і інші частини кімнати. Ми можемо, однак, розглядати рух того ж тіла і щодо Сонця або будь-якої певної зірки, тільки ми повинні вперед точно домовитися, щодо чого саме ми розглядаємо рух нашого предмета "[2] (с. 17). Тут ключова фраза "переміщення може відбуватися лише щодо будь-яких інших матеріальних тіл", а ключове слово "лише". Цим все сказано. Іншими словами, рух щодо нематеріальної точки простору в цьому світогляді навіть не мислиться. І це сказано через 3 століття після Ньютона! Що означає все ще не відбулося розуміння сенсу ньютоновского перевороту. Не тільки самим Ньютоном, але, на жаль, і нашими сучасниками. Ще цитата: "Зупиняючись докладніше на першому законі Ньютона, треба поставити питання: щодо якої системи відліку (який координатної системи) встановлюється той спокій або то рівномірний і прямолінійний рух, про який йде мова в першому законі Ньютона. Сам Ньютон мав на увазі, що мова йде про деяке абсолютному русі в абсолютному просторі. Він писав: "Абсолютна простір по всій своїй суті, безвідносно до чого б то не було зовнішнього, залишається завжди однаковим і нерухомим ... Абсолютна рух є переміщення тіла з одного абсолютного його місця в інше". Така точка зору метафізічна і не відповідає дійсності. Властивості об'єктивно існуючого реального простору визначаються самою матерією. Положення тіл і їх рух, як ми вже підкреслювали, можуть бути визначені лише щодо інших матеріальних тіл; по відношенню до різних тіл одне і те ж тіло може рухатися по-різному. Спостереження показують, що перший закон Ньютона справедливий не по відношенню до кожної системі відліку. Розглянемо кілька прикладів. Покладемо, що системою відліку є прямолінійно і рівномірно рухається вагон. Тоді, якщо відволіктися від струсів, перший закон Ньютона виконується: покояться щодо вагона тіла не приходять в рух без впливу на них з боку інших тіл і т.д. Але варто вагону почати загортати, гальмувати або прискорювати хід, як з'являться явні порушення першого закону Ньютона: покоїлися до того тіла можуть відхилитися або впасти без видимого впливу на них з боку оточуючих тел. Візьмемо в якості системи відліку земну кулю; в цьому випадку перший закон Ньютона виконується набагато точніше, ніж в разі рухомого вагона, де навіть при рівномірному русі позначається тряска, але і тут досить тонкі спостереження над деякими процесами (хитання маятників, поширення повітряних і океанських течій і т.д.) виявляють відхилення від першого закону Ньютона або, вірніше, від наслідків з нього. Але якщо ми виберемо в якості системи відліку геліоцентричну систему, початок якої вміщено на Сонце, а осі направлені на певні зірки, то в такому випадку перший закон Ньютона виконується практично цілком точно. Система відліку, по відношенню до якої виконаний перший закон Ньютона, носить назву інерціальній системи. Сам перший закон Ньютона іноді називається принципом інерції. Як зазначено, інерційної системою практично цілком точно є геліоцентрична система; інерційної буде також і будь-яка система, що рухається щодо неї рівномірно і прямолінійно. Будь-яка ж система, що має відносно однієї з інерційних систем прискорення, сама не буде інерційної "(там же, с. 45). Відвернемося від обраного сумнівного прикладу прямолінійного руху, утвореного двома обертаннями - щодо центру Землі і разом з нею - щодо Сонця. А також і від того, що є негативною рисою науки: ще не з'ясувавши до пуття, що це таке, відразу ж починати вести мову про різні його види. Стосовно до ІСО - міркувати про інших ІСО. Начебто тільки про них ще й залишилося щось там ще з'ясувати. Цим навмисно затуманюється питання про незнання сенсу самої ІСО, ІСО як такої. Хоча б однієї з них. Що і називається йти від питання. У розглянутому прикладі цікаво прийняття вагона в якості ІСО. Якби справа відбувалася в відкритому просторі, то це, взагалі кажучи, могло б бути допустимо. Якщо, наприклад, маса вагона 10 т, а маса тіла 1 кг і обидва вони представлені точкової тілами, розташованими на невеликій відстані один від одного (а зовсім не приміщенням малого тіла всередині великого, можливо, поблизу його центру мас). Тільки лише в цьому випадку ІСО з відомою точністю дійсно може бути представлена СО вагона. Але справа то в тому, що це відбувається зовсім не в відкритому просторі, а на поверхні Землі, роль якої повністю втрачена. Вона ж така, що ІСО є СО саме Землі. Якраз тому під час відсутності тертя висмикування вагона з-під тіла не змінює положення цього тіла в ІСО. Що і утворює переміщення тіла, що спочиває в ІСО, щодо вагона. Так само невірно прийняття СО Сонця в якості ІСО.Сонце, звичайно, набагато масивніше Землі, але і відстань до нього настільки перевищує земний радіус, що створюване їм прискорення 0,6 см / с2 нехтує в порівнянні з прискоренням 980 см / с2, створюваним Землею. Тут правильну відповідь може бути тільки один. ІСО в даному випадку є тільки СО Землі, що іменується також птолемеевской СО. Обидва ці невірних затвердження залишаються непоміченими лише тому, що нікому і в голову не приходить подивитися на них уважніше, а не вполглаза. Ось що ще в цьому тексті привертає увагу. Як ІСО приймається то Земля, а разом з нею, отже, і система Птолемея, начебто спростована Коперником, то Сонце і разом з ним система Коперника. При цьому залишається абсолютно незрозумілим, як і коли відбувається перехід від однієї системи до іншої. Оскільки перемогли коперниканцем найсуворіше табу навіть сама згадка про те, що "спростована" система Птолемей і досі щосили застосовується в масштабі Землі, досягаючи навіть Місяця. Притому що і сама система Коперника вірна лише для планет сонячної системи, а зовсім не для зірок, що взаємодіють з Сонцем. Або Галактики, де Сонце саме є такою ж "планетою". Не кажучи вже про атомарних або внутрішньоатомних рухах, в яких поняття ІСО і зовсім неясно. Тут навіть придумано ціле "пояснення": в такому масштабі закони класичної механіки вже чомусь не діють. Що просто означає: це покрито мороком туману. І на закінчення Птолемей і Коперник, будучи, ймовірно, сучасниками [3, 4], мали, по суті, однакову світогляд, властиве своєму часу. Чи прийняти Землю або ж Сонце в якості нерухомої СО в общем-то не суттєво. Але навіть і сам Ньютон, фактично котрий улаштував принципово іншу ІСО, теж, звичайно, не розумів радикального значення її відкриття. Зрозуміло чому. Перший з його законів просто невірний, а третій є всього лише визначенням фізичної величини сили. Четвертий же - закон всесвітнього тяжіння варто і зовсім особняком, без розуміння його тісному зв'язку з трьома іншими. З їх сукупності випливає, що справжня ІСО зовсім не є нерухомою, а навпаки рухається, причому прискорено, щодо кожного з взаємодіючих тіл! В цьому і полягає найбільше світоглядне відкриття, розуміння якого досі ще не досягнуто. А "нерухомі" земна або навпаки сонячна СО - це всього лише окремі випадки "правильного" співвідношення взаємодіючих мас і просторового масштабу. Птолемєєвськая система утворена частиною простору, що примикає до будь-якого матеріального об'єкта. Вона є навіть у галілеївських об'єктів, хоча і вироджується в плівку нульової товщини, що покриває їх поверхню. У ньютоновских об'єктів це вже не плівка, а навколишня їх сферична частина простору. З Птолемєєвськая радіусом R п, визначеним масою mн ньютоновского об'єкта. Розташованого в її центрі. У масштабі Rп дію ньютоновских об'єктів на галілеївські об'єкти перевищує дію Сонця. Тому тут, як і раніше вірна система Птолемея. І в цьому масштабі вона ніколи не була і не може бути спростована ніякими Коперника. І точно так само в коперниковской великому масштабі Rк (масштабі сонячної системи), де сонячний вплив перевищує вплив всіх інших ньютоновских об'єктів, із заданою точністю вірна система Коперника. І її теж не спростує і не може спростувати ніякої Птолемей. Але тільки за вирахуванням локальних частин простору, що примикають до самих ньютоновским об'єктів. Утворюють безліч птолемеевскую зон. Іншими словами, система Коперника не є безперервною. Охоплюється нею простір нагадує головку сиру, що містить безліч планетарних "дірок" з центрами, утвореними ньютоновскими об'єктами. Внутрішній простір яких описується системами Птолемея, незалежними між собою. В цьому і тільки цьому сенсі можна говорити про те, що система Коперника дійсно спростувала систему Птолемея. Помилково екстраполіруемую в надмірно великий для неї масштаб сонячної системи. Поблизу ж ньютоновских об'єктів система Птолемея анітрохи не постраждала, і можна навіть сказати, що в точності так само спростовує систему Коперника. Додамо, що система Птолемея утворена безліччю локальних фрагментів, що примикають до кожного ньютоновскому об'єкту. Обставина, можливо, і зовсім не помічається учасниками фізичних суперечок. А в загальному випадку не праві обидва, тому що справжня ISO не є ні земний, ні сонячної СО. Тому історична суперечка Птолемея-Коперника залишається завершеним до з'ясування діапазонів мас і просторового масштабу, в межах яких кожна з систем з відомою точністю є справедливою. Це з'ясування ставить, нарешті, крапку в цьому тривалому і неадекватному історичній суперечці. Список літератури www.sciteclibrary.ru/rus/catalog/pages/8444.html. С.Е.Фріш, А.В. Тіморева "Курс загальної фізики" Том I. Фізичні основи механіки. Видання шосте, виправлене. Державне видавництво техніко-теоретичної літератури, Москва, 1955. Г.В. Носівський, А.Т. Фоменко "Реконструкція загальної історії. Дослідження 1999 - 2000 років, Нова хронологія "ФІД" Діловий експрес ", Москва, 2000, с. 378 -379. Г.В. Носівський, А.Т. Фоменко "Введення в Нову Хронологію (Який зараз століття?)", Изд. "Крафт", Москва, 2001, с. 98. |
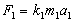 ,
,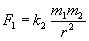 .
. і
і  , Потрібно, як сказано, вирішити цю систему.
, Потрібно, як сказано, вирішити цю систему.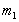 , Є силою тяжіння:
, Є силою тяжіння: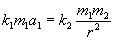 .
.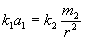 .
. .
.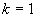
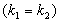 , Приходимо до наступного визначення маси:
, Приходимо до наступного визначення маси: 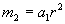 .
.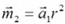 .
. ):
):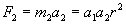 .
.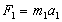
 ,
, ,
,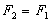 ,
,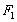 ,
, 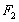 ,
, 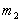 .
. ,
,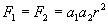 .
.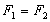 , Наприклад, замінюється рівністю
, Наприклад, замінюється рівністю 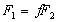 , (
, ( 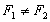 ), То тут слід почати з того, що невідомо,
), То тут слід почати з того, що невідомо, 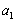 ,
, 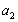 , Носить найменування інерціальній системи відліку (ІСО).
, Носить найменування інерціальній системи відліку (ІСО).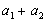 .
.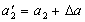 (
( 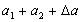 .
.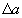 від додавання тіла 3 в ІСО і в СО1 має однакову величину і, отже, його можна визначити вимірюванням в СО1.
від додавання тіла 3 в ІСО і в СО1 має однакову величину і, отже, його можна визначити вимірюванням в СО1.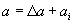 ,
,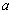 - прискорення i-го тіла щодо тіла 3,
- прискорення i-го тіла щодо тіла 3,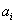 - прискорення i-го тіла щодо ІСО,
- прискорення i-го тіла щодо ІСО,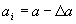 ,
,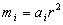 ,
,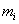 - маса i-го тіла.
- маса i-го тіла. при цьому характеристики рухів служать характеристиками тел.
при цьому характеристики рухів служать характеристиками тел.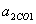 , Залежне від тіла 1 (відповідно в СО2 тіло 1 має прискорення
, Залежне від тіла 1 (відповідно в СО2 тіло 1 має прискорення 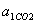 , де
, де 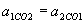 ).
).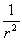 .
.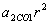 .
.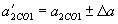 .
.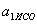 .
.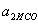 .
.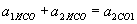 .
.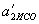 , В СО1 -
, В СО1 - 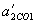 .
.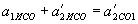 .
.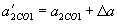 .
.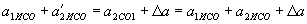 , Тобто зміни прискорень тіла 2 в СО1 і в ІСО однакові, рівні
, Тобто зміни прискорень тіла 2 в СО1 і в ІСО однакові, рівні 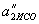 , В СО1 -
, В СО1 - 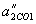 .
. .
.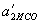 ,
, 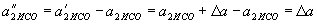 ,
,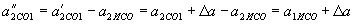 .
.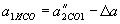 .
.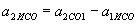 .
.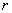 прискорення
прискорення 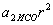 вже не залежить ні від тіла 2, ні від відстані
вже не залежить ні від тіла 2, ні від відстані 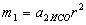 .
.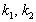 приймаються рівними одиниці:
приймаються рівними одиниці: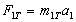 ,
,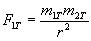
 томсонових еталонів (g має довільне, відмінне від одиниці числове значення).
томсонових еталонів (g має довільне, відмінне від одиниці числове значення).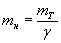 .
.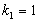 :
: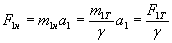 .
.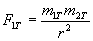 ,
, 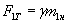 і
і 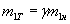 ,
, 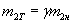 ,
,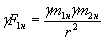 або
або 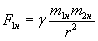 , звідки
, звідки 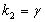 .
.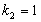 :
: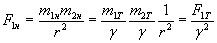 .
.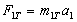 в новій системі одиниць:
в новій системі одиниць: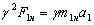 або
або 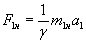 звідки:
звідки: 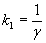 .
.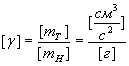 .
.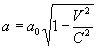 , (
, ( 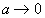 при
при  ),
),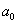 - прискорення при відносних швидкостях
- прискорення при відносних швидкостях 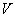 , Багато менших швидкості світла
, Багато менших швидкості світла 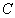 , То і сила взаємодії
, То і сила взаємодії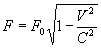 , (
, ( 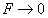 при
при 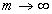 за формулою
за формулою 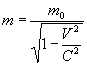 , оскільки
, оскільки 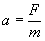 .
.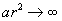 , Тобто
, Тобто 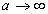 і
і 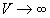 , Що виключається, оскільки
, Що виключається, оскільки 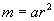 ,
, 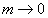 :
: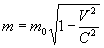 .
.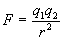 .
.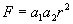 , де
, де 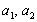 - прискорення, що набувають
- прискорення, що набувають або
або 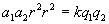 .
.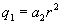 ,
,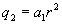 ,
,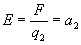 є прискорення, що купується пробним тілом.
є прискорення, що купується пробним тілом. .
.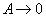 .
. , Відповідно і робота
, Відповідно і робота 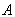 має кінцеве значення.
має кінцеве значення.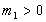 ,
,  ,
, 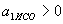 ,
, 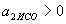 .
.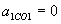 ,
,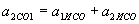 .
.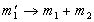 ,
, 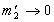 ,
, 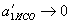 ,
, 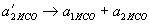 .
. .
.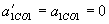 ,
,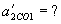
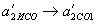 , То, отже,
, То, отже,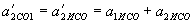 .
.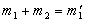 , А також переносу в СО1 самої ІСО.
, А також переносу в СО1 самої ІСО.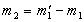 .
.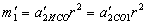 .
.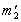 (Пробного тіла).
(Пробного тіла).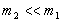 , що означає:
, що означає: 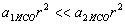 або
або 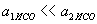 .
.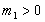 ,
, 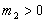 ,
, 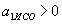 ,
, 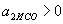 ,
,  ,
,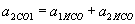 .
.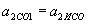 .
.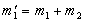 ,
, 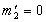 ,
, 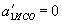 ,
, 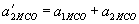 .
.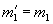 ,
, 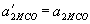 .
.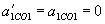 ,
, 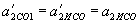 ,
,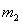 до тіла 1 великої маси
до тіла 1 великої маси 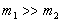 приєднання маси
приєднання маси 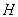 (де
(де 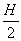 .
.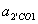 ,
,  , причому
, причому 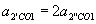 .
.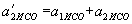 ,
,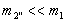 ,
, 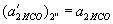 .
.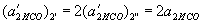 .
.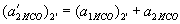 .
.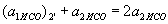 ,
, 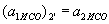 , Тобто
, Тобто 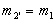 .
.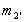 і однаковою геометрії з галілеївсько об'єктом повинен мати масу
і однаковою геометрії з галілеївсько об'єктом повинен мати масу 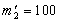
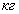 ,
, 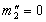 .
.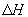 тілом 2 'тіла 2 "в СО1 становить:
тілом 2 'тіла 2 "в СО1 становить: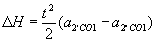 ,
,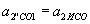 ,
, 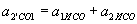 , Тобто
, Тобто 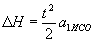 .
.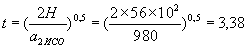 с,
с,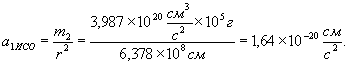
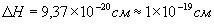 .
.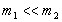 , То при вимірах в СО1 галилеевский об'єкт масою
, То при вимірах в СО1 галилеевский об'єкт масою 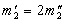 дійсно має в 2 рази більшим прискоренням
дійсно має в 2 рази більшим прискоренням 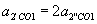 , В повній відповідності з "спростовуваних" положенням Аристотеля.
, В повній відповідності з "спростовуваних" положенням Аристотеля.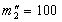 г і ядра
г і ядра 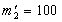 кг масу Землі, разом з розташованої на ній Пізанської вежею і експериментатором-фізиком, рівну, скажімо,
кг масу Землі, разом з розташованої на ній Пізанської вежею і експериментатором-фізиком, рівну, скажімо, 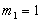 м
м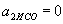 маємо:
маємо: 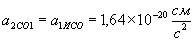 .
.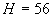 м буде пройдений за час
м буде пройдений за час 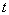 , Рівне:
, Рівне: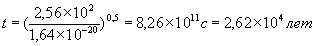 ,
,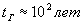 пройдена висота Пізанської вежі складе:
пройдена висота Пізанської вежі складе: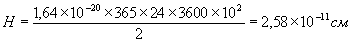
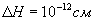 .
.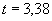 c, рівне часу спостереження реального Галілея:
c, рівне часу спостереження реального Галілея: .
.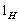 ,
, 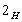 :
: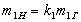 ,
,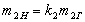 ,
,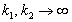 .
.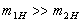 , а
, а 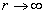 .
.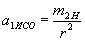 ,
, 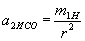 , оскільки
, оскільки 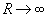 , При деяких
, При деяких 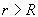 обидва прискорення
обидва прискорення 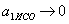 ,
, 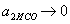 , Весь час залишаючись при цьому
, Весь час залишаючись при цьому  ,
, 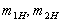 починаючи з деякого мінімального
починаючи з деякого мінімального 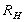 ) ІСО знову, як і в разі галилеевского об'єкта
) ІСО знову, як і в разі галилеевского об'єкта 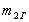 приводиться до СО1.
приводиться до СО1.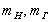 :
: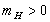 ,
, 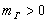 ,
, 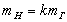 ,
, 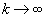 ,
,  ,
,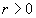 .
.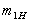 ,
, 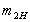 з істотно нерівними масами
з істотно нерівними масами  :
: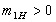 ,
, 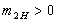 ,
, 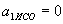 ,
, 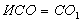 ,
, 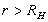 ,
,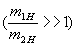 .
.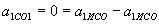 ,
,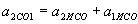 .
.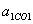 і
і 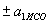 .
.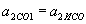 .
.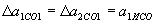 , де
, де 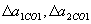 - похибка наближення, яку вносить заміною істинної ІСО наближеною
- похибка наближення, яку вносить заміною істинної ІСО наближеною 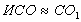 .
.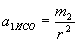 , Маємо:
, Маємо: 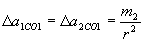 .
.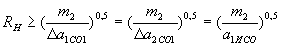 .
.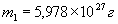 , Тіло 2 - Місяць,
, Тіло 2 - Місяць, 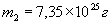 ,
, 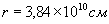 , Маємо:
, Маємо: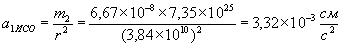 ,
,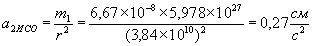 .
.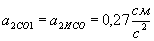 .
.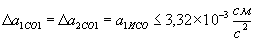 .
.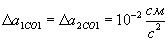 маємо:
маємо: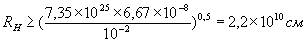 .
.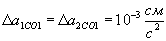 мінімальне ньютонівської відстань для даної пари 1, 2 ньютоновских об'єктів становить вже
мінімальне ньютонівської відстань для даної пари 1, 2 ньютоновских об'єктів становить вже 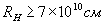 , Що не забезпечується в реальному парі, тобто в даному випадку прийняття СО1 як наближеною ISO не допустимо.
, Що не забезпечується в реальному парі, тобто в даному випадку прийняття СО1 як наближеною ISO не допустимо. при будь-якому (галілеївських або ньютоновском) відстані, де 1 - ньютоновский об'єкт? ".
при будь-якому (галілеївських або ньютоновском) відстані, де 1 - ньютоновский об'єкт? ". ,
,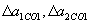 , Можна було прийняти
, Можна було прийняти 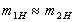 , При будь-якій відстані між ними, крім
, При будь-якій відстані між ними, крім 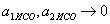 , Тобто взаємодія припиняється, внаслідок чого в якості місцевої ІСО може бути прийнята як СО1, так і СО2 ".
, Тобто взаємодія припиняється, внаслідок чого в якості місцевої ІСО може бути прийнята як СО1, так і СО2 ".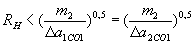 ".
".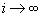 c масами
c масами 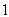 ,
,  .
.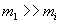 , То його СО1 з урахуванням
, То його СО1 з урахуванням 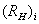 і заданої точності наближення може бути прийнята в якості місцевої ІСО для кожної заданої пари.
і заданої точності наближення може бути прийнята в якості місцевої ІСО для кожної заданої пари.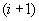 ньютоновскими взаємодіючими об'єктами.
ньютоновскими взаємодіючими об'єктами.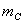 якого багато більше маси
якого багато більше маси 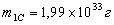 ,
, 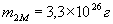 ,
, 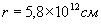 :
: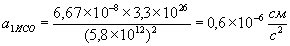 ,
, 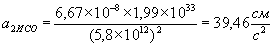 .
.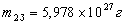 ,
, 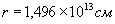 , Аналогічні обчислення дають:
, Аналогічні обчислення дають: 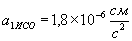 ,
, 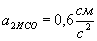 ; для пари Сонце-Юпітер, де
; для пари Сонце-Юпітер, де 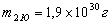 ,
, 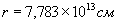 :
: 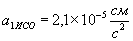 ,
,  , і т.д.
, і т.д.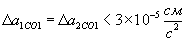 .
.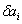 для даної пари ньютоновских об'єктів
для даної пари ньютоновских об'єктів 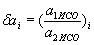 становить: для пари Сонце-Меркурій:
становить: для пари Сонце-Меркурій: 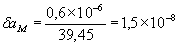 , Для пари Сонце-Земля
, Для пари Сонце-Земля 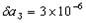 ; для пари Сонце-Юпітер
; для пари Сонце-Юпітер 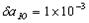 .
.