Історія статистики
|
Скачати 94.32 Kb.
|
|
| Дата конвертації | 07.10.2019 |
| Розмір | 94.32 Kb. |
| Тип | курсова робота |
|
|
-
Навігація по даній сторінці:
- Тема 2. Ряди розподілу. Статистичні таблиці
- Тема 3. Графічне зображення статистичних даних
- Тема 4. Абсолютні і відносні статистичні величини
- Тема 5. Середні величини
- Тема 7. Показники варіації
- Тема 9. Взаємозвязки явищ
- Тема 10. Вибіркове спостереження
- Тема 11. Закони розподілу
|
Роботу виконав: Serk МГТУ «Станкин» 2003 рік Тема 1. Статистичні дані. угруповання Статистичні дані є другим етапом статистичного дослідження після спостереження. Вона полягає в тому, що первинні матеріали, отримані в результаті спостереження, обробляються, зводяться разом і характеризуються підсумковими узагальнюючими показниками. Складовими елементами зведення є: 1) програма зведення; 2) підрахунок групових підсумків; 3) оформлення кінцевих результатів зведення у вигляді таблиць і графіків. Програма статистичного зведення містить перелік груп, на які розчленована досліджувана сукупність за певними ознаками, а також перелік показників, необхідних для характеристики кожної групи. Програма зведення має, як правило, вид вільних статистичних таблиць, які слід заповнити розрахунковими даними. У зведенні статистичного матеріалу важлива ланка займають угруповання, так як простий підрахунок підсумків без розподілу одиниць сукупності на групи за тими або іншими ознаками не дає повної характеристики об'єкта вивчення. До статистичних угруповань вдаються при вирішенні наступних завдань: а) аналіз структури досліджуваної сукупності; б) виявлення зв'язків і взаємозалежностей між економічними явищами. Для вирішення першого завдання будують структурні угруповання. Для вирішення другого завдання будують аналітичні угруповання. Угруповання бувають прості і комбінаційні. Проста угруповання утворюється за однією ознакою, комбінаційна - за двома і більше ознаками. Можна здійснювати угруповання як за кількісною ознакою, так і по атрибутивному. В кількісної угрупованню группіровочний ознака виражається варіантами чисел. У атрибутивної угрупованню группіровочний ознака кількісного вираження не має, так як характеризує якість досліджуваного явища. В економіко-статистичному аналізі робляться угруповання як з рівними, так і з нерівними інтервалами. При побудові угруповання з рівними інтервалами величину інтервалу груп визначають за такою формулою:
де Xmax - максимальне значення ознаки в досліджуваній сукупності; Xmin - мінімальне значення ознаки в досліджуваній сукупності; n - число груп. При виборі числа груп необхідно враховувати наступне: 1) в кожну групу може потрапити за можливості досить велике число одиниць; 2) число одиниць в групах не повинно різко відрізнятися один від одного, тобто має бути приблизно одного порядку; 3) груп має бути не більше 6-7. Угруповання з нерівними інтервалами доцільно застосовувати в тих випадках, коли вихідні статистичні дані різняться на досить значну величину, тобто коли занадто великий розмах варіації в вихідної сукупності. Розглянемо приклад на побудову аналітичної угруповання. Таблиця 1.1 Дані про вартість основних фондів і товарної продукції підприємств
За звітними даними 20 промислових підприємств потрібно побудувати аналітичну угруповання для встановлення залежності обсягу товарної продукції від середньої річної вартості основних виробничих фондів (табл. 1.1). Для побудови угруповання виділимо группіровочний ознака. Таким группіровочним ознакою є середня річна вартість основних виробничих фондів. Приймемо число груп за цією ознакою n = 5. Величину інтервалу в групах визначаємо за наведеною вище формулою. Тоді h = (396 - 198): 5 = 39,6 млн. Руб. Утворити групи підприємств по середньої річної вартості основних виробничих фондів. Нижню межу першого інтервалу складе мінімальна величина группировочного ознаки 198 млн. Руб. Верхня межа першого інтервалу складе 198 + 39,6 = 237,6 млн. Руб. При угрупованнях по безперервно варьирующим кількісними ознаками кордон інтервалів позначають так, що верхня межа попереднього інтервалу служить нижньою межею наступного інтервалу. Таким чином, нижньою межею другого інтервалу буде величина 237,6 млн. Руб., А верхньою межею даного інтервалу - величина 237,6 + 39,6 = 277,2 млн. Руб. Аналогічно визначаються межі наступних інтервалів. Отримуємо наступні інтервали для 5 груп підприємств по середньої річної вартості основних виробничих фондів: 198 - 237,6; 237,6 - 277,2; 277,2 - 316,8; 316,8 - 356,4; 356,4 - 396,0. В першу групу увійшло 6 підприємств; в другу - 2; в третю - 6; в четверту - 4; в п'яту - 2. Так як за умовою завдання необхідно встановити залежність обсягу товарної продукції від середньої річної вартості основних виробничих фондів, то в кожній виділеній групі визначаємо сумарну величину обсягу товарної продукції за сукупністю підприємств в групі і в розрахунку на одне підприємство. За першою групою підприємств із середньою річною вартістю основних виробничих фондів від 198 млн. Руб. до 237,6 млн. руб. обсяг товарної продукції складе: 399,6 + 348,3 + 378,3 + 350,1 + 590,4 + 315,0 = 2381,7 млн. руб., і в розрахунку на одне підприємство: 2381,7: 6 = 396,9 тис. руб. Аналогічні розрахунки проводимо по інших групах. Результати розрахунків зведемо в табл. 1.2. Таблиця 1.2 Розрахунок середнього обсягу товарної продукції за групами підприємств
На основі побудованої угруповання видно чітка залежність обсягу товарної продукції від середньої річної вартості основних виробничих фондів підприємства. Використовуючи умову даного завдання, побудуємо структурну угруповання. Для побудови структурної угруповання необхідно сформувати групи з другою ознакою - величиною товарної продукції. Візьмемо число груп n = 5; межі інтервалів груп визначаємо за формулою величини інтервалу угруповання h, де
Групи підприємств, утворені за обсягом товарної продукції, такі: 315,0 - 441,52; 441,52 - 568,04; 568,04 - 694,56; 694,56 - 821,08; 821,08 - 947,6. Надалі, здійснюючи розподіл підприємств в групах по середньої річної вартості основних виробничих фондів на підгрупи за обсягом товарної продукції, сформуємо структурну угруповання (табл. 1.3). На основі структурної угруповання чітко видно розподіл підприємств за обсягом товарної продукції в залежності від тієї чи іншої середньої річної вартості виробничих фондів. Таблиця 1.3 Структурна угруповання підприємств за двома показниками
Підприємства зосереджені, головним чином, по діагоналі, що ще раз підкреслює тенденцію збільшення обсягу товарної продукції при зростанні вартості основних виробничих фондів підприємства. Тема 2. Ряди розподілу. Статистичні таблиці В результаті обробки і систематизації первинних статистичних даних отримують ряди цифрових показників, які характеризують окремі сторони досліджуваних явищ. Ці ряди називають статистичними. Статистичні ряди ділять на два види: ряди розподілу та ряди динаміки. Ряди розподілу характеризують розподіл одиниць сукупності за будь-якою ознакою. Ряди динаміки характеризують зміну досліджуваних явищ у часі. Ряди розподілу, в свою чергу, діляться на атрибутивні та варіаційні. Атрибутивний ряд розподілу утворюється за якісною ознакою. Варіаційний ряд утворюється за кількісною ознакою. Серед варіаційних рядів розподілу виділяють дискретні та інтервальні ряди. У дискретному варіаційному ряду розподілу окремі варіанти мають певні конкретні значення. В інтервальному варіаційному ряду варіанти коливаються в певних межах. Варіаційні ряди зображують в системі прямокутних координат у вигляді діаграм. Дискретні варіаційні ряди зображують у вигляді так званого полігону розподілу. Варіанти відкладаються на осі абсцис, частоти - на осі ординат. Точки перетину з'єднуються відрізками прямий. Інтервальні варіаційні ряди зображують у вигляді гістограми. На осі абсцис відкладають межі інтервалів, на осі ординат - число одиниць сукупності, що припадає на одиницю ширини інтервалу (щільність розподілу). В інтервалах будують прямокутники. Для зображення інтервальних варіаційних рядів з рівними інтервалами на осі абсцис відкладають межі інтервалів, а на осі ординат - число одиниць сукупності в даному інтервалі. Будують прямокутники з рівними інтервалами. Інтервальний варіаційний ряд можна зображувати також у вигляді кумуляти. На осі абсцис відкладають межі інтервалів, на осі ординат - наростаючі частоти, відповідні верхніх меж інтервалів. Точки перетину з'єднують відрізками прямої. Статистичні ряди як результат статистичного зведення та угруповання завжди викладаються у вигляді статистичних таблиць. Статистична таблиця являє собою форму найбільш раціонального, наочного і систематизованого викладу цифрових результатів зведення і обробки статистичного матеріалу. При побудові статистичних таблиць слід чітко розмежовувати статистичне підмет і статистичне присудок. Статистичним підметом таблиці є сам об'єкт (перелік його одиниць або їх груп), що характеризується числовими показниками. Статистичним присудком таблиці є числові показники, які характеризують досліджуваний об'єкт. Статистичне підлягає розташовують, як правило, в рядках, статистичне присудок - в графах таблиці. Залежно від будови підлягає розрізняють три види таблиць: прості, групові, комбінаційні. Прості (перечневий) таблиці в підметі містять перелік розглянутих об'єктів. Групові таблиці в підметі містять угруповання одиниць досліджуваного об'єкта, утворену з якого-небудь одній ознаці. Комбінаційні таблиці в підметі містять угруповання одиниць, утворену з двох і більше ознаками. При побудові таблиць слід строго дотримуватися певних правил: 1. Кожна таблиця повинна бути пронумерована і мати заголовок, який в короткій формі повинен відображати зміст таблиці, місце і час явища. 2. У таблиці використовуються тільки загальноприйняті скорочення. 3. У таблиці повинні бути приведені одиниці виміру. Якщо одиниця виміру загальна, вона виноситься справа над таблицею в дужках. 4. Цифрові дані доцільно скорочувати. 5. До таблиці можна робити примітки, які мають у своєму розпорядженні під таблицею з виноскою під рискою. 6. При перенесенні таблиці на інший аркуш, графи таблиці доцільно позначати арабськими цифрами. Тема 3. Графічне зображення статистичних даних Графіками в статистиці називають умовні зображення числових величин і їх співвідношень у вигляді різних геометричних фігур в системі прямокутних координат. Графіки є засобом узагальнення і аналізу статистичних даних. За допомогою графіків виявляються основні тенденції розвитку економічних явищ і взаємні зв'язки між явищами. Статистичні графіки розрізняють за змістом і способу побудови. За змістом зображуваних статистичних показників графіки ділять на наступні види: 1) графіки порівняння; 2) графіки структури; 3) графіки динаміки; 4) графіки виконання плану; 5) графіки взаємопов'язаних показників. За способом побудови розрізняють стовпчикові, стрічкові, лінійні, кругові, квадратні, секторні діаграми. Для побудови графіків порівняння доцільно використовувати лінійну, стовпчикові, стрічкову, квадратну, кругову діаграми. Столбиковая діаграма зображується у вигляді стовпчиків, підстави яких відкладаються на осі абсцис, висота - на осі ординат. Ширина стовпчиків довільна, але однакова. Лінійна діаграма зображується у вигляді лінії, що з'єднує точки перетину розрахункових величин в ряді динаміки. Стрічкову діаграму доцільно будувати в тому випадку, якщо об'єкт характеризується двома показниками, як правило, протилежними за змістом. У стрічкової діаграмі на відміну від столбиковой стовпчики розташовані не вертикально, а горизонтально в системі прямокутних координат. Квадратну діаграму доцільно будувати в тому випадку, коли між порівнюваними показниками різниця настільки велика, що встановлення відповідного масштабу виявляється скрутним. Сторона кожного квадрата визначається як корінь квадратний з відповідної величини. Тоді площа квадратів візуально буде характеризувати ту чи іншу вихідну величину. Кругові діаграми будуються аналогічно квадратах. Радіус кола є корінь квадратний з певної величини. Для побудови графіків структури, як правило, використовують стовпчикові і секторні діаграми. Особливістю побудови секторної діаграми є те, що обсяг кола в секторної діаграмі приймається за 100 відсотків, а величини секторів пропорційні процентному відношенню складових частою до їх загального підсумку. Побудова графіків динаміки здійснюється, як правило, за допомогою столбиковой або лінійної діаграм. Графічне зображення показників виконання плану можна здійснити у вигляді лінійної, стрічкової і столбиковой діаграм в системі прямокутних координат. При цьому на осі абсцис відкладають періоди динаміки, на осі ординат - показники виконання плану. Для графічного зображення показників виконання плану часто використовують числові сітки з двома сполученими шкалами. Одна шкала характеризує виконання плану в абсолютних величинах, інша - у відносних величинах (відсотки виконання плану). Числові сітки використовують для характеристики виконання планового завдання за період динаміки або в розрізі цехів і дільниць. Побудова графіків взаємопов'язаних показників, один з яких дорівнює добутку двох інших, можна здійснювати за допомогою так званих "знаків Варзара". "3нак" будується поза системою прямокутних координат у вигляді прямокутника, основа якого пропорційно одним показником - співмножник, висота - іншому. При побудові графіків (діаграм) в системі прямокутних координат необхідно дотримуватися наступних правил: 1. Кожен графік повинен мати назву, яку розміщують під ним. У назві в короткій формі слід відобразити зміст, місце і час явища. Всі графіки нумеруються. 2. Осі координат повинні бути названі і мати одиниці виміру. 3. На числової осі слід відкладати тільки цілі числа і в рівному масштабі (наприклад: 20; 40; 60 і т.д., або 1500; 3000; 4500 і т.д.). Закінчуватися числова вісь повинна тією величиною, яка трохи більше максимальної величини у вихідній сукупності. 4. Якщо на одній числової осі необхідно розташувати величини, що відносяться до одного і того ж явища, але різко відрізняються один від одного за абсолютним значенням, числову вісь можна розірвати знаком (≈), що означає розрив масштабу. 5. Якщо необхідно відобразити на одному графіку (в одній системі прямокутних координат) два-три явища, то вводять стільки ж додаткових числових осей (осей ординат). Кожна числова вісь повинна мати свою розмірність і свій масштаб. Тема 4. Абсолютні і відносні статистичні величини Під абсолютними величинами в статистиці розуміють показники, які характеризують розміри (рівні, обсяги) досліджуваних економічних явищ. Абсолютні величини є вихідною базою статистичного аналізу. На відміну від абсолютних величин відносні величини є величинами похідними і розраховуються на основі абсолютних. У статистичному аналізі використовують наступні види відносних величин: величини динаміки, величини виконання плану, величини структури, величини координації, величини інтенсивності, величини порівняння. При вивченні відносних величин динаміки необхідно, перш за все, усвідомити їх роль в характеристиці розвитку явища в часі. Слід звернути увагу на характер бази порівняння (постійна, змінна). Наведемо приклад розрахунку відносних величин динаміки (табл. 4.1). Таблиця 4.1 Випуск товарної продукції на підприємстві
Обчислимо відносні величини динаміки з постійною базою порівняння, прийнявши за базу січень: 1426,9: 1390,7 = 1,026 '100 = 102,6%; 1492,6: 1390,7 = 1,073 '100 = 107,3% і т.д. Обчислимо відносні величини динаміки зі змінною базою порівняння, використовуючи співвідношення кожного наступного місяця до попереднього: 1426,9: 1390,7 = 1,026; 1492,6: 1426,9 = 1,046 '100 = 104,6% і т.д. При обчисленні відносних величин структури слід усвідомити їх зв'язок з угрупованням статистичних даних. Наведемо приклад розрахунку (табл. 4.2). Таблиця 4.2 Розподіл робочих за тарифними розрядами
Для характеристики структури робочих за тарифними розрядами (у відсотках) визначають питому вагу чисельності робітників за відповідними розрядами в загальній чисельності робітників. Так, питома вага чисельності робітників 1 розряду становить (3: 197) '100 = 1,5% і т.д. (Див. Табл. 4.2). При обчисленні відносних величин координації за базу порівняння приймається будь-яка одна частина досліджуваного явища, а решта частини співвідносяться з нею. Для прикладу скористаємося даними табл. 4.2. Якщо взяти за базу порівняння чисельність робітників 2 розряду, тоді відносні величини координації складуть: При обчисленні відносних величин інтенсивності необхідно пам'ятати, що вони є іменованими показниками: так, коефіцієнт фондовіддачі показує, який обсяг продукції припадає на одиницю вартості основних виробничих фондів; показник продуктивності праці характеризує величину обсягу продукції в розрахунку на одиницю трудових витрат і т.д. При обчисленні відносних величин порівняння потрібно запам'ятати, що порівняно між собою піддаються однойменні величини, що відносяться до різних об'єктів, взяті, як правило, за один і той же період часу. Наприклад, співвідношення випуску продукції на двох підприємствах в звітному періоді склала 102%. Тема 5. Середні величини Середні величини в статистиці виконують роль узагальнюючих показників, що характеризують досліджувану сукупність одиниць по будь-якою ознакою. У статистиці використовують різні види середніх величин: середня арифметична проста, середня арифметична зважена; середня гармонійна, середня геометрична; структурні середні - мода і медіана. Під час вивчення цієї теми особливу увагу слід звернути на те, що кожен вид середньої величини визначається в залежності від конкретного економічного умови і від поставленого завдання. В іншому випадку середня величина дасть помилковий результат і буде спотвореною характеристикою досліджуваної статистичної сукупності. Середня величина розраховується за якісно однорідної сукупності, значення якої приблизно одного порядку. Це - основна умова застосування середньої. Не можна забувати про те, що середні величини в статистиці є величинами іменованими і виражаються в тих же одиницях, в яких виражена ознака. Необхідно також усвідомити значення середніх моди і медіани, за допомогою яких вивчають структуру досліджуваної сукупності. Проілюструємо на конкретних прикладах порядок розрахунку кожного виду середніх величин. 1. Розподіл робітників-наладчиків ділянки одного з цехів промислового підприємства за стажем роботи та кваліфікаційними розрядами характеризується такими даними: Таблиця 5.1
Визначити: а) середній розряд робочих кожної вікової групи; б) середній стаж робітників ділянки. Рішення: а) Для знаходження середнього розряду робочих кожної вікової групи слід застосувати середню арифметичну зважену:
в якості ваги (m) виступає конкретний розряд робітників. Так, для робітників зі стажем роботи до 10 років середній тарифний розряд складе:
І так далі по іншим віковим групам. б) Для знаходження середнього стажу робітників на ділянці застосовують ту ж середню арифметичну зважену, але вже для інтервального ряду розподілу. Причому, як "x" будуть серединні значення ознаки в групах, а в якості ваги (m) приймають чисельність робітників відповідної групи:
2. За наступними даними розподілу робочих цеху по відсотку виконання місячного завдання визначити моду і медіану. Таблиця 5.2 Дані про виконання виробничого завдання
Модою в статистиці називають найбільш часто зустрічається в досліджуваній сукупності значення ознаки. Отже, в даній задачі модальним буде інтервал від 100 до 105 відсотків, так як на нього припадає найбільше число робочих (20 чол.). Моду визначають за формулою: Mo = x 0 + де x 0 і x 1 - відповідно нижня і верхня межі модального інтервалу; m 2 - частота модального інтервалу; m 1 і m 3 - частоти інтервалу, відповідно, попереднього і наступного за модальним. Підставимо значення в формулу: Mo = 100 + Інакше кажучи, найбільше число робочих виконують місячне завдання на 103,1%. Медианой в статистиці називають серединне значення ознаки в досліджуваній сукупності. Отже, медіанного є інтервал, на який припадає 50% накопичених частот даного ряду, що за умовою задачі 42: 2 = 21. У нашій задачі медіана знаходиться в інтервалі від 100 до 105%, так як на даний інтервал доводиться накопичена частота 23. Медіану визначають за формулою: Me = x 0 + де x 0 і x 1 - відповідно нижня і верхня межі медіанного інтервалу; N - сума частот ряду; N 0 - сума частот, що накопичилася до початку медіанного інтервалу; N 1 - частота медіанного інтервалу. Підставами відповідне значення в формулу: Me = 100 + Таким чином, 50% всіх робочих виконують виробниче завдання менш ніж на 104,5%; 50% - більш ніж на 104,5%. Тема 6. Ряди динаміки Рядами динаміки називають ряди, які характеризують зміну явища в часі. Ряди динаміки бувають моментні і інтервальні. Моментні ряди характеризують зміна явища в динаміці на певний момент часу (частіше - на початок або кінець періоду). Інтервальні ряди характеризують зміна явища в динаміці за певний період часу (місяць, квартал, рік). В економічному аналізі використовують аналітичні показники динаміки. До них відносять абсолютний приріст, середній абсолютний приріст, темп зростання, темп приросту, середній темп зростання, абсолютне значення одного відсотка приросту. Дані показники широко використовуються в статистичній практиці, що викликає необхідність ретельного вивчення порядку їх розрахунку. Розглянемо на прикладі розрахунок аналітичних показників ряду динаміки (табл. 6.1). Таблиця 6.1 Дані про виробництво в цеху
Абсолютний приріст (D) визначається як різниця між звітним і попереднім рівнями ряду динаміки, тобто за формулою: D = y i - y i -1, де y i, y i -1 - рівні ряду динаміки. Так, наприклад, абсолютний приріст продукції цеху в лютому в порівнянні c січнем склав: 244 - 236 = 8 тис. Руб., А в березні в порівнянні з лютим: 246 - 244 = 2 тис. Руб. і т.д. Середній абсолютний приріст (
де n - число рівнів ряду динаміки; y 1 і y n - відповідно перший і останній рівні ряду динаміки. Темп зростання (Т р) визначається за формулою: Т р = де y 0 - рівень ряду динаміки, взятий за базу порівняння. Темп зростання розраховується за принципом ланцюгових і базисних співвідношень. В тому числі, коли за базу порівняння приймається попередній період - це ланцюгові показники темпу зростання, коли порівняння здійснюється з будь-яким іншим рівнем ряду динаміки, узятим за базу порівняння - базисні темпи зростання. Так, в лютому в порівнянні з січнем випуск продукції в цеху склав: Т р2 = (244: 236) '100% = 103,4%, а в березні в порівнянні з лютим: Т р3 = (246: 244)' 100% = 100,8% і т.д. Якщо за базу порівняння взяти січень, то випуск продукції в цеху в березні в порівнянні з січнем склав: (246: 236) '100% = 104,2%, а в квітні в порівнянні з січнем: (249: 236)' 100% = 105,5% і т.д. Темп приросту (Т пр) на відміну від темпу зростання характеризує відносний приріст явища в звітному періоді в порівнянні з тим рівнем, з яким здійснюється порівняння і визначається: Т пр = Т р - 100. Так, в березні обсяг продукції цеху в порівнянні з лютим збільшився на 0,8% (100,8 - 100), а по бою з січнем - на 4,2% (104,2 - 100) і т.д. Абсолютне значення одного відсотка приросту (А) характеризує абсолютний еквівалент одного відсотка приросту і визначається за формулою: А = Так, в березні абсолютне значення одного відсотка приросту склало: (2: 0,8) = 2,4 млн. Руб. і т.д. Середній темп зростання (
або
де x 1, x 2,..., x n - коефіцієнти динаміки по відношенню до попереднього періоду; n - число коефіцієнтів динаміки; k - число абсолютних рівнів ряду динаміки. Так, за перше півріччя середній річний темп зростання продукції в цеху склав: Один з найважливіших питань, що виникають при вивченні рядів динаміки - це виявлення тенденції розвитку економічної закономірності в динаміці. Для цієї мети застосовуються різноманітні статистичні методи, зокрема, метод укрупнення інтервалів, метод ковзної середньої, метод аналітичного вирівнювання. Найбільш простим у використанні є метод укрупнення інтервалів, заснований на укрупненні періодів часу, до яких відносяться рівні ряду. Виявлення тенденції здійснюється за новим укрупнених ряду динаміки. Інший метод - метод ковзної середньої полягає в заміні початкових рівнів ряду динаміки середніми арифметичними, знайденими за способом ковзання, починаючи з першого рівня ряду з поступовим включенням наступних рівнів. Найбільш досконалим методом виявлення тенденції ряду динаміки є метод аналітичного вирівнювання, який полягає в заміні початкових рівнів ряду новими, знайденими в часі "t" побудовою аналітичного рівняння зв'язку. Розглянемо на прикладі можливості застосування кожного з методів вирівнювання при виявленні тенденції ряду динаміки. Відомі такі дані виконання програми ділянкою "молдинги" цеху ЗІЛ-130 пресового корпусу за 1989 г. (табл.6.2). Таблиця 6.2
1. За методом укрупнення інтервалів маємо нові укрупнені поквартально рівні ряду динаміки: у 1 = 18,6 + 17,3 + 18,9 = 54,8; y 2 = 18,2 + 17,9 + 19,1 = 55,2 і т.д. Вирівняний ряд динаміки набуде вигляду: 54,8 55,2 56,3 57,5. Тобто спостерігається парне виражена тенденція збільшення випуску молдингів цехом за 1989 р 2. Вживаючи ті ж дані, можна застосувати метод ковзної середньої, використовуючи семічленную ковзаючу середню. тоді:
Вирівняний за допомогою семичленной ковзної середньої ряд динаміки набуде вигляду: 18,5 18,4 18,6 18,7 18,8 19,0. Таким чином, підтверджується тенденція збільшення випуску молдингів протягом 1989 р 3. Використовуючи метод відліку від умовного нуля введемо умовне позначення часу "t", надавши йому певні значення так, щоб Σt = 0 (див. Табл. 6.2). Судячи з виявленої за допомогою двох попередніх методів тенденції випуску молдингів протягом року, можна сказати, що найбільш імовірна лінійна залежність даного розподілу від часу "t" і даним розподілу відповідає рівняння прямої Для знаходження параметрів a 0 і a 1 використовуємо систему рівнянь
так як Σt = 0, про маємо a 0 = a 1 = Отже, рівняння прямої набуде вигляду:
Тема 7. Показники варіації Поряд із середньою величиною, що характеризує типовий рівень варьирующего ознаки, біля якого коливаються окремі значення ознаки, розглядають показники варіації (коливання) ознаки, що дозволяють кількісно виміряти величину цієї коливання. До показників варіації відносять: розмах варіації, середнє лінійне відхилення, дисперсію, середньоквадратичне відхилення, коефіцієнт варіації. Найпростішим показником варіації є розмах варіації, який розраховується за такою формулою: R = Xmax - Xmin, де Xmax, Xmin - відповідно, максимальне і мінімальне значення ознаки в досліджуваній сукупності. Розмах варіації характеризує діапазон коливань ознаки в досліджуваній сукупності і вимірюється в тих же одиницях, в яких виражена ознака. Розраховують середнє лінійне відхилення, яке буває незважене і зважене. Якщо кожне значення ознаки зустрічається в сукупності один раз, то застосовується формула середнього лінійного відхилення невиваженого:
де x - значення ознаки; n - кількість варіант. Якщо є деяка повторюваність значень ознаки, то застосовується формула середнього лінійного відхилення зваженого:
де m - частота. Середнє лінійне відхилення характеризує абсолютний розмір коливання ознаки біля середньої і вимірюється в тих же одиницях, в яких виражена ознака. Найбільш точним показником варіації є середнє відхилення. Для його визначення попередньо розраховують показник дисперсії. Дисперсія невиважена визначається за формулою: σ 2 = Дисперсія зважена визначається за формулою: σ 2 = Тоді, відповідно, для розрахунку середнього квадратичного відхилення невиваженого використовують формулу: σ = а для розрахунку середнього квадратичного відхилення зваженого - наступну формулу: σ = Як і середнє лінійне відхилення, середнє квадратичне відхилення характеризує абсолютний розмір коливання ознаки біля середньої, однак є більш точною характеристикою. На відміну від середнього лінійного і середнього квадратичного відхилення коефіцієнт варіації є мірою відносної коливання ознаки біля середньої і характеризує ступінь однорідності ознаки в досліджуваній сукупності. Він визначається за формулою: υ σ = Якщо досліджувану сукупність одиниць розчленувати на групи, то маємо право вважати, що загальна дисперсія всієї сукупності варіює (змінюється) під впливом дисперсій для кожної окремої групи, так званих групових або приватних дисперсій і груповий дисперсії. Ці дисперсії пов'язані між собою правилом складання дисперсій. При використанні правила складання дисперсій в економічному аналізі за величиною приватної дисперсії може вирішуватися завдання виявлення найбільш ефективної у виробництві системи (форми, структури і т.п.) організації праці, її оплати та т.п. Приватні або групові дисперсії характеризують коливання досліджуваного ознаки в кожній окремій групі і визначаються за такою формулою:
і їх середня величина
де i = 1, 2, ..., n - номер групи; m i - чисельність одиниць у групі. Межгрупповая дисперсія характеризує коливання приватних середніх близько загальної середньої γ 2 = При дотриманні правила складання дисперсій повинна дотримуватися рівність: σ 2 = Проілюструємо розрахунок показників варіації за даними про розподіл робочих за стажем роботи (табл. 7.1). 1. R = Xmax - Xmin = 14 - 10 = 4 роки, тобто діапазон коливання стажу робітників в досліджуваній сукупності становить 4 роки. 2.
Таблиця 7.1 Стаж роботи робочих
В середньому на 1,1 року відхиляється стаж окремих робочих від середнього стажу за сукупністю. 3. σ 2 = σ = Величина σ = 1,3 року характеризує коливання стажу роботи робітників в даній сукупності: υ σ = Таким чином, на 11,4% варіює склад робочих за стажем роботи в досліджуваній сукупності. Тема 8. Індекси У статистиці індексами називають відносні величини, що показують співвідношення показників в часі, просторі, а також фактичних показників з плановими. Індекси вимірюються у відсотках. Для деяких простих, одиничних явищ, які допускають безпосереднє порівняння, будують індивідуальні індекси. Дня явищ складних, що складаються з безпосередньо несумірних елементів, будують зведені індекси. Так, для характеристики динаміки виробництва конкретного виду продукції, застосовується індивідуальний індекс. Якщо ж дослідника цікавить динаміка випуску всієї продукції підприємства, то в цьому випадку будується зведений індекс, так як окремі види продукції підприємства безпосередньо несумірні. Розроблена статистикою теорія індексів дозволяє вирішити такі завдання: 1) визначати співвідношення показників в часі, просторі, фактичних даних з плановими; 2) виявляти абсолютні результати вимірювання показників в аналогічних напрямках; 3) визначати відносне і абсолютне вплив окремих факторів на таку зміну за умови, що фактори представлені у вигляді твору. В теорії індексів найбільш часто використовуються наступні позначення: I - індивідуальний індекс; J - зведений індекс. Порядок побудови індивідуальних індексів дуже простий: в чисельнику дробу записується показник на рівні звітного періоду, в знаменнику - на рівні базисного періоду. наприклад: I p = де I p - індивідуальний індекс цін; I t - індивідуальний індекс трудомісткості; I q - індивідуальний індекс продукції; p 1 і p 0 - ціна одиниці продукції, відповідно, в звітному і базисному періодах, руб .; t 1 і t 0 - трудомісткість виготовлення одиниці продукції, відповідно, в звітному і базисному періодах, год; q 1 і q 0 - кількість виробленої продукції, відповідно, в звітному і базисному періодах, шт. Існують ланцюгові і базисні індивідуальні індекси. У ланцюгових індексах кожний наступний період порівнюється з попереднім, наприклад:
Неважко помітити, що множення ланцюгових індексів дає в підсумку порівняння явищ, розділених поруч проміжків часу (базисні індекси):
Природно, якщо в задачі відомий базисний індекс і якісь з ланцюгових, то для знаходження інших ланцюгових індексів необхідно робити поділ. Слід знати, що індекси динаміки, планового завдання та виконання плану пов'язані між собою відомим з теорії відносних величин співвідношенням: Iдінамікі = Iпл. завдання'Iвиполненія плану. Якщо в задачі потрібно знайти абсолютне зміна якогось явища, то воно визначається як різниця між чисельником і знаменником індексу: (p 1 - p 0); (t 1 - t 0) і т.д. Якщо при цьому ставиться завдання визначити, як впливає ця зміна на якийсь многофакторное явище, то знайдена різниця між чисельником і знаменником якісного індексу (цін, трудомісткості і т.п.) множиться на відповідний кількісний фактор (кількість продукції, чисельність працюючих і т .п.) на рівні звітного періоду. Різниця між чисельником і знаменником кількісного індексу (продукції, чисельності працюючих і т.п.) множиться на відповідний якісний фактор (трудомісткість і т.п.) на рівні базисного періоду: (p 1 - p 0) q 1 - розмір економії (перевитрати) грошових коштів від зниження (підвищення) цін; (t 1 - t 0) q 1 - розмір збільшення (зменшення) витрат праці на виробництво продукції від підвищення (зниження) трудомісткості; (q 1 - q 0) p 0 - розмір економії (перевитрати) грошових коштів від зміни обсягу випуску продукції; (q 1 - q 0) t 0 - розмір збільшення (зменшення) витрат праці на виробництво продукції від зміни обсягу випуску продукції і т.д. На відміну від індивідуальних індексів, зведені індекси являють собою результат порівняння складних явищ, що складаються з безпосередньо несумірних елементів. Зведені індекси являють собою співвідношення сум творів індексованих величин і їх соизмеритель. Як соизмеритель можуть виступати: трудомісткість виготовлення продукції (t), ціна одиниці продукції (p), собівартість одиниці продукції (z). Назва зведеного індексу визначається постійно змінюваних (індексовані) показником. Індексований показник записують в чисельнику на рівні звітного періоду, в знаменнику - на рівні базисного періоду або на рівні планового завдання. Якщо індексується якісний показник (ціна, трудомісткість, собівартість), то відповідний йому кількісний соизмеритель фіксується на рівні звітного періоду. Якщо індексується кількісний показник, то відповідний йому якісний соизмеритель фіксується на рівні базисного періоду або на рівні планового завдання. Виходячи з цього, зведений індекс цін запишеться: J p = зведений індекс трудомісткості: J t = зведений індекс собівартості: J z = зведений індекс фізичного обсягу продукції: J q = J q = J q = Індекси цін, трудомісткості і собівартості продукції відносяться до індексів постійного складу, так як q = const. Індекси фізичного обсягу продукції незалежно від соизмерителя відносяться до індексів структурних зрушень, так як враховується зміна в асортименті та обсязі продукції. У тому випадку, коли в зведеному індексі індексується сам показник і його соизмеритель, обидва складових в чисельнику записуються на рівні звітного періоду, в знаменнику - на рівні базисного періоду, а назва зведеного індексу визначається індексованими складовими. Так, зведений індекс обсягу продукції у вартісному вираженні запишеться J qp = Такі індекси відносяться до індексів змінного складу, так як варіюють обидва складових. У статистичному аналізі використовується взаємозв'язок індексів змінного складу і структурних зрушень, яка проявляється у вигляді двох властивостей індексів. Перше властивість індексів: індекс змінного складу дорівнює добутку індексів постійного складу і структурних зрушень: J qp = J q ∙ J p; J qt = J q ∙ J t; J qz = J q ∙ J z; Друге властивість індексів: різниця чисельника і знаменника індексу змінного складу дорівнює сумі різниць чисельника і знаменника індексів постійного складу і структурних зрушень: Dqp (qp) = Dqp (q) + Dqp (p); Σq 1 p 1 - Σq 0 p 0 = (Σq 1 p 0 - Σq 0 p 0) + (Σq 1 p 1 - Σq 1 p 0); Dqt (qt) = Dqt (q) + Dqt (t); Σq 1 t 1 - Σq 0 t 0 = (Σq 1 t 0 - Σq 0 t 0) + (Σq 1 t 1 - Σq 1 t 0); Dqz (qz) = Dqz (q) + Dqz (z); Σq 1 z 1 - Σq 0 z 0 = (Σq 1 z 0 - Σq 0 z 0) + (Σq 1 z 1 - Σq 1 z 0). Розглянемо приклад: По одному з підрозділів промислового підприємства відомі такі дані (табл. 8.1). Таблиця 8.1
Розрахуємо індивідуальні індекси продукції і індивідуальні індекси цін. Індивідуальні індекси з відповідних видів продукції складуть: I q (А) = I q (Б) = I q (В) = Тобто в звітному періоді в порівнянні з базисним вироблено продукції виду "А" і "Б", відповідно, на 33,3% більше, а виду "В" - на 100% більше. Індивідуальні індекси цін за відповідними видами продукції складуть: I p (А) = I p (Б) = I p (В) = Тобто ціна одиниці продукції виду "А" в звітному періоді в порівнянні з базисним знизилася на 12,5% (100 - 87,5), виду "Б" - на 25% (100 - 75) і виду "В" - на 20% (100 - 80). Індивідуальні індекси конкретного виду продукції у вартісному вираженні, відповідно, складуть: I p (А) = I p (Б) = I p (В) = Таким чином, обсяг продукції у вартісному вираженні виду "А" в звітному періоді в порівнянні з базисним збільшиться на 16,7% (116,7 - 100), виду "В" - на 60% (160 - 100) і виду "Б "- залишиться без зміни (100 - 100). Для того, щоб відповісти на питання, як зменшився обсяг всієї продукції підприємства в звітному періоді в порівнянні з базисним, необхідно розрахувати зведені індекси продукції, цін і фізичного обсягу продукції. Зведений індекс обсягу продукції у вартісному вираженні складе: J qp = Зведений індекс цін складе: J p = Зведений індекс фізичного обсягу продукції складе: J q = Використовуючи перше властивість індексів, маємо: J qp = J q ∙ J p; 125% = 1,5 '0,833' 100%. Використовуючи друга властивість індексів, маємо: Dqp (qp) = Dqp (q) + Dqp (p), тобто (25 - 20) = (30 - 20) + (25 - 30) або (+5) = (+10) + (-5). Таким чином, можна зробити висновок: обсяг продукції у вартісному вираженні збільшився в цілому на 25%, або на 5 '(25 - 20) тис. Руб., В тому числі за рахунок зниження цін на 16,7% (83,3 - 100) обсяг знизився на 5 тис. руб. (25 - 30), а за рахунок збільшення фізичного обсягу продукції на 50% (150 - 100) обсяг продукції у вартісному вираженні збільшився на 10 тис. Руб. Тема 9. Взаємозв'язки явищ Перший етап вивчення зв'язку явищ - виділення основних причинно-наслідкових зв'язків і відділення їх від другорядних. Другий етап - побудова моделі. Останній етап - інтерпретація результатів. Ознаки-аргументи називаються факторами, а ознаки-функції - результатами (результативними ознаками). Зв'язки між явищами ділять за ступенем тісноти зв'язку (повна або функціональний зв'язок, неповна або статистичний зв'язок), у напрямку (пряма, зворотна), по аналітичного вираженню (лінійна, нелінійна). Для виявлення зв'язку, її характеру, напряму використовують методи приведення паралельних даних, балансовий, аналітичних угруповань, графічний. Суть методу приведення паралельних даних: призводять два ряди даних про двох ознаках, зв'язок між якими хочуть виявити, і за характером змін роблять висновок про наявність зв'язку. Балансовий метод полягає в побудові балансів - таблиць, де підсумок однієї частини дорівнює підсумку інший. Методи аналітичних угруповань і графічний викладені у відповідних темах. Зручна форма викладу даних - кореляційний таблиця (табл. 9.1). Таблиця 9.1 кореляційна таблиця
Таблиця показує, що частоти концентруються у діагоналі, що йде з лівого верхнього кута в правий нижній. Це вказує на те, що зв'язок між кількістю обслуговуваних робітницею верстатів і її годинниковою виробленням тканини пряма (зі збільшенням кількості обслуговуваних верстатів збільшується вироблення) або близька до прямої (концентрація частот йде майже по прямій лінії). За даними таблиці можна розрахувати середню вироблення по кожній з семи груп робітниць, виділених за кількістю обслуговуваних верстатів. Позначивши ці середні значення через Дані таблиці і результати розрахунків можна зобразити графічно за допомогою поля кореляції. Ламана лінія на графіку (лінія значень Показники тісноти зв'язку. Для оцінки тісноти зв'язку застосовується ряд показників, одні з яких називаються емпіричними або непараметричних, інші (виводяться строго математично) - теоретичними. Коефіцієнт знаків (коефіцієнт Фехнера) обчислюється на підставі визначення знаків відхилень варіантів двох взаємопов'язаних ознак від їх середніх величин. Якщо число збігів знаків позначати через a, кількість розбіжностей - через b, а сам коефіцієнт - через i, то можна записати формулу цього коефіцієнта так:
Коефіцієнт кореляції рангів (коефіцієнт Спірмена) розраховується не за значенням двох взаємопов'язаних ознак, а по їх рангах наступним чином: ρ x / y = 1 - де d i - різниці рангів; n - число пар рангів. Для визначення тісноти зв'язку між трьома і більше ознаками застосовується рангові коефіцієнт згоди - коефіцієнт конкордації, який обчислюється за формулою: w = де m - кількість факторів; n - число спостережень; S - сума квадратів відхилень рангів. Величина коефіцієнта конкордації більше 0,5 показує, що між досліджуваними величинами є тісна залежність. Якщо при визначенні тісноти зв'язку за допомогою наведених рангових коефіцієнтів є зв'язкові ранги, тобто якщо двом або більше показниками присвоєно один і той же ранг, то розрахунки проводяться за формулами: коефіцієнт Спірмена: ρ x / y = 1 - коефіцієнт конкордації: w = де T = При дослідженні соціальних явищ і процесів велике значення має вивчення якісних показників і ознак, які не мають кількісної оцінки:
Для визначення тісноти зв'язку двох якісних ознак, кожен з яких складається тільки з двох груп, застосовуються коефіцієнти асоціації і контингенции. Для їх обчислення будується таблиця, яка показує зв'язок між двома явищами, кожне з яких має бути альтернативним, тобто що складається з двох якісно відмінних один від одного значень ознаки (наприклад, хороший, поганий). Коефіцієнти обчислюються за формулами: A = K = Коефіцієнт контингенции завжди менше коефіцієнта асоціації. Зв'язок вважається підтвердженою, якщо A ³ 0,5, або K³ 0,3. Якщо кожен з якісних ознак складається більше ніж з двох груп, то для визначення тісноти зв'язку можливе застосування коефіцієнта взаємної спряженості Пірсона. Цей коефіцієнт обчислюється за формулою: C = де j 2 - показник взаємної спряженості. Розрахунок коефіцієнта взаємної спряженості проводиться за наступною схемою:
Расчетj 2 проводиться так: по першому рядку по другому рядку по третьому рядку Отже, j 2 = L 1 + L 2 + L 3 - 1. Інтерпретація непараметрических коефіцієнтів зв'язку в деяких випадках, особливо коли вони мають негативне значення, скрутна. Їх абсолютні значення можуть змінюватися в межах від 0 до 1. Чим ближче абсолютні значення до одиниці, тим тісніше зв'язок між досліджуваними ознаками. Кореляція і регресія. Традиційні методи кореляційно-регресійного аналізу дозволяють не тільки оцінити тісноту зв'язку, а й висловити цей зв'язок аналітично. Застосуванню кореляційно-регресійного аналізу повинен передувати якісний, теоретичний аналіз досліджуваного соціально-економічного явища або процесу. Зв'язок між двома факторами аналітично виражається рівняннями: прямий гіперболи параболи статечної функції Параметр a 0 показує усереднене вплив на результативну ознаку неврахованих (не виділені для дослідження) чинників. Параметр a 1 - коефіцієнт регресії показує, на скільки змінюється в середньому значення результативної ознаки при збільшенні факторного на одиницю. На основі цього параметра обчислюються коефіцієнти еластичності, які показують зміну результативної ознаки у відсотках в залежності від зміни факторної ознаки на 1%: Е = a 1 ∙ Для визначення параметрів рівнянь використовується метод найменших квадратів, на підставі якого будується відповідна система рівнянь. Тіснота зв'язку при лінійної залежності вимірюється за допомогою лінійного коефіцієнта кореляції: r = а при криволінійної залежності за допомогою кореляційного відносини: h = Розрахунок коефіцієнтів регресії дещо ускладнюється, якщо ряди по досліджуваним чинникам згруповані, а зв'язок криволінійна. Якщо залежність між двома факторами виражається рівнянням гіперболи
то система рівнянь для визначення параметрів a 0 і a 1 така: na 0 + a 1 Σ a 0 Σ Для визначення параметрів рівняння регресії, вираженого статечної функцією n ∙ lga 0 + a 1 Σlgx = Σlgy; lga 0 Σlgx + a 1 Σ (lgx) 2 = Σlgy ∙ lgx. Залежність між трьома і більше факторами називається множинною або багатофакторної кореляційної залежністю. Лінійна зв'язок між трьома факторами виражається рівнянням:
а система нормальних рівнянь для визначення невідомих параметрів a 0, a 1, a 2 буде наступною: na 0 + a 1 Σx + a 2 Σz = Σy; a 0 Σx + a 1 Σx 2 + a 2 Σzx = Σyx; a 0 Σz + a 1 Σxz + a 2 Σz 2 = Σyz. Тіснота зв'язку між трьома факторами вимірюється за допомогою множинного (сукупного) коефіцієнта кореляції: R = де r ij - парні коефіцієнти кореляції між відповідними факторами. Для більш поглибленого аналізу обчислюються приватні коефіцієнти кореляції. Дисперсійний аналіз зв'язку. При невеликому числі спостережень дослідити вплив одного або декількох факторних ознак на результативний можна, використовуючи методи дисперсійного аналізу. Дисперсійний аналіз проводиться розрахунком дисперсій: загальної, груповий і внутрішньогруповий. Загальну дисперсію називають дисперсією комплексу, міжгрупова - факторной, внутригрупповую - залишкової. Дисперсійний аналіз полягає в порівнянні факторной і залишкової дисперсій. Якщо відмінність між ними значимо, то факторний ознака, тобто ознака, покладений в основу угруповання, робить істотний вплив на результативний. При дослідженні впливу на результативний ознака тільки одного факторного, тобто однофакторного комплексу дисперсії обчислюються: дисперсія комплексу факторная дисперсія залишкова дисперсія де n - 1, r - 1, n - r - відповідні числа ступенів свободи; r - число рівнів (груп). На підставі дисперсій проводиться розрахунок критерію Фішера F p. Якщо розрахункове значення більше табличного, тобто F p> F a, то істотність впливу факторної ознаки підтверджується. Тема 10. Вибіркове спостереження Головними питаннями теорії вибіркового спостереження, які вимагають практичного закріплення на основі вирішення завдань і виконання вправ, є: - визначення меж випадкової помилки репрезентативності для різних типів вибіркових характеристик з урахуванням особливостей відбору; - визначення обсягу вибірки, що забезпечує необхідну репрезентативність вибіркової характеристики, з урахуванням особливостей відбору. Помилка репрезентативності, або різниця між вибіркової і генеральної характеристикою (середньої, часткою), що виникає в силу несплошного спостереження, в основі якого лежить випадковий відбір, розраховується як межа найімовірніше помилки. Як рівня гарантійної ймовірності зазвичай береться 0,954 або 0,997. Тоді межа помилки визначається величиною подвійною чи потрійною середньої помилки вибірки: D = 2m при P = 0,954; D = 3m при P = 0,997, або в загальному вигляді D = tm (t - коефіцієнт, пов'язаний з імовірністю, що гарантує результат). Величина середньої помилки вибірки різна для окремих різновидів випадкового відбору. При найбільш простій системі - власне-випадковому повторному відборі - середня помилка визначається наступними формулами: індивідуальний відбір: m = де σ 2 - загальна дисперсія ознаки; n - число відібраних одиниць спостереження; груповий (гніздовий, серійний) відбір: m = де δ 2 - міжгрупова дисперсія; r - число відібраних груп (гнізд, серій) одиниць спостереження. При практичних розрахунках помилок репрезентативності необхідно враховувати наступне: 1. Замість генеральної дисперсії використовується відповідна вибіркова дисперсія. Так, замість загальної дисперсії частки у генеральній сукупності береться загальна дисперсія частости:
2. У разі бесповторного способу відбору (а також механічного) слід мати на увазі поправки (K) до помилки повторної вибірки на бесповторном відбору: K = Очевидно, що користуватися цією поправкою доцільно лише тоді, коли відносний обсяг вибірки становить помітну частину генеральної сукупності (не менше 10%, тоді K £ 0,95). 3. При районованих відборі з типових груп одиниць генеральної сукупності використовується середня з приватних (групових) дисперсій. Так, при індивідуальному відборі, пропорційному розмірам типових груп, маємо: D = 2m = де n i - обсяг вибірки в i-й групі. Визначення помилок вибіркових характеристик дозволяє встановити найімовірніше кордону знаходження відповідних генеральних показників: для середньої: де
для частки: p = w ± Dw, де p - генеральна частка; w - вибіркова частка (частость); Dw - помилка вибіркової частки. Приклад. З ймовірністю 0,954 потрібно визначити межі середньої ваги пачки чаю для всієї партії, що надійшла в торговельну мережу, якщо контрольна вибіркова перевірка дала такі результати (перші дві графи табл. 10.1). Таблиця 10.1 Результати зважування чаю
1. Середня вага пачки чаю по вибірці:
2. Вибіркова дисперсія ваги пачки чаю: σ 2 = 3. Середня помилка вибіркової середньої:
4. Межа для помилки з імовірністю 0,954: D = 2m = 0,174 г »0,2 м 5. Межі генеральної середньої:
Таким чином, з імовірністю 0,954 можна стверджувати, що вага пачки чаю в середньому для всієї партії не більше 49,9 г і не менше 49,5 м Визначення обсягу вибірки при заданої її точності є проблемою, зворотної розглянутої нами - визначення помилки вибірки при даному її обсязі. Формула обсягу вибірки виходить з відповідної формули граничної помилки. Так, отримуємо для індивідуального бесповторного відбору: n = групового бесповторного відбору: r = При вирішенні завдань на визначення необхідного обсягу вибірки слід мати на увазі, що замість генеральної дисперсії певного виду береться її оцінка - приблизне значення, отримане з того чи іншого джерела. Розглянемо наступний загальний приклад. Приклад. Потрібно визначити абсолютний і відносний обсяги індивідуального відбору для дослідження генеральної частки, щоб помилка частости з ймовірністю 0,954 не перевищувала 0,02, якщо вибірка проводиться з генеральної сукупності обсягу: а) 1000; б) 100000 одиниць. Використовуючи формулу n = а) n = б) n = Тема 11. Закони розподілу Кінцевою метою обробки інформації методами математичної статистика, якщо мова йде про великих вибірках, є отримання закону розподілу досліджуваної випадкової величини. Це пов'язано з тим, що закон розподілу є фактично, тим апаратом, який дозволяє визначити ймовірність появи (або, навпаки, непоявленія) випадкової величини в той чи інший період часу або ймовірність того, що випадкова величина потрапить в той чи інший інтервал її можливих значенні . Цей етап статистичної обробки є одним з найбільш важливих, так як помилка при виборі того чи іншого закону розподілу призводить до помилок при подальшому вирішенні практичних завдань. Якщо проаналізувати всі етапи статистичної обробки, то можна зробити висновок, що тягнуть за собою найбільш суттєві помилки, а, отже, найбільш відповідальними, є етапи, на яких вирішуються наступні завдання: 1. Чи можливе об'єднання кількох малих або середніх вибірок в одну. 2. Відкидати чи враховувати різко відрізняються результати. 3. Чи справедливо зроблене припущення про закон розподілу випадкової величини. Розглянемо ці етапи більш детально. 1. Так як для встановлення закону розподілу необхідні великі вибірки, то на практиці часто постає питання про об'єднання кількох вибірок, кожна з яких мала для вирішення поставленого завдання і отримання однієї загальної вибірки, задовольняє пред'явленим до неї вимогам. Тому, що взагалі властиво для статистичної обробки, будь-яка з неправильних рішень (як позитивне, так і негативне) з приводу об'єднання вибірок призводить до небажаних результатів, або до неможливості встановити закон розподілу, якщо вибірки не об'єднуються, або до неправильного висновку про характер закону розподілу . Для вирішення цього завдання використовують критерії, за допомогою яких з різною формулюванням фактично дається відповідь на один і той же питання: чи належать або не належать досліджувані вибірки однієї генеральної сукупності, тобто автоматично вирішується завдання про можливість або неможливість їх об'єднання. Як правило, всі ці критерії засновані на порівнянні вибіркових характеристик (вибіркових дисперсій або середніх величин) між собою або з відповідними генеральними характеристиками. У більшості випадків використання цих критеріїв передбачає нормальний або логарифмічно-нормальний закон розподілу для кожної вибірки. При інших же законах розподілу ці критерії є некоректними і їх використання може призвести до помилкових результатів. Найбільш використовуваними є наступні критерії: а) критерії, засновані на порівнянні дисперсій: критерій б) критерії, засновані на порівняннях середніх величин: критерій Стьюдента (t), критерій Z та інші. Для всіх критеріїв в якості нульової гіпотези (H 0) висувається припущення про приналежність вибірки генеральної сукупності або про однорідність вибірок між собою. 2. При наявності вибірки, задовольняє вимогам щодо її придатності для встановлення закону розподілу перед тим, як приступити до визначення статистичних характеристик, необхідно перевірити, чи належать до даної вибірці її члени, що різко відрізняються від більшості даних, якщо такі є. Така перевірка строго обов'язкове, так як будь-який невірний рішення щодо різко відрізняються результатів призводить до спотворення виду кривої закону розподілу і до подальших помилок, про які вже йшлося вище. Описана перевірка також здійснюється за допомогою відповідних критеріїв: критерію Груббс (для малих вибірок), критерію Ірвіна і деяких інших. Як нульової гіпотези у всіх випадках приймається припущення про те, що різко виділяються результати належать даній вибірці. 3. Заключною і самої трудомісткою перевіркою є перевірка гіпотез про вид функції розподілу або, що те ж, про відповідність передбачуваного закону теоретичного розподілу емпіричному. Ця перевірка здійснюється за допомогою так званих критеріїв згоди. Існують критерії для перевірки відповідності як передбачуваного нормальному або логарифмічно-нормальному закону розподілу, так і будь-якого іншого закону розподілу. Найбільш використовуваними при практичних розрахунках є такі критерії: а) критерій Пірсона (χ 2); він справедливий при великих обсягах вибірок і для будь-яких законів розподілу; б) критерій Колмогорова-Смирнова (Du); цей критерій використовується для перевірки гіпотези про відповідність емпіричного розподілу будь-якого теоретичного закону розподілу із заздалегідь відомими параметрами, що накладає обмеження на його використання. У той же час Du є більш потужним, ніж критерій χ 2; в) критерій Крамера-Мізеса (w 2); цей критерій використовується для обсягів вибірок 50 £ n £ 200 і є більш потужним, ніж χ 2, однак, при його застосуванні потрібно більший обсяг обчислень. Тому при n> 200 цей критерій доцільно використовувати тільки в тих випадках, коли перевірки гіпотези за іншими критеріями не призводять до безумовним результатами; г) критерій Шапіро-Вілкса (W); він призначений для перевірки гіпотези про нормальний або логарифмічно нормальному законі розподілу при обмеженому обсязі вибірки (n £ 50) і є більш потужним, ніж інші критерії. Укрупнено порядок проведення статистичної обробки інформації можна представити таким чином: після вирішення питання про обсяг вибірки і приналежності до неї різко відрізняються результатів, будується гістограма, розраховуються статистичні характеристики досліджуваної випадкової величини, і встановлюється закон її розподілу. При вирішенні технічних і економічних завдань існує досить широке коло законів розподілу, яким підкоряються ті чи інші процеси. До них відносяться закони Вейбулла, Релея, експоненціальне, гамма-розподілу, однак, найпоширенішими є нормальний (Гаусса) і логарифмічно-нормальний закони розподілу. Отримавши математичне вираз закону розподілу, тобто співвідношення, яке встановлює зв'язок між можливими значеннями випадкової величини і відповідними їм ймовірностями, можна стверджувати, що з ймовірнісної точки зору, випадкова величина описана повністю. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
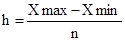 ,
,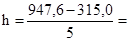 126,52 млн. Руб.
126,52 млн. Руб.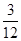 = 0,25;
= 0,25; 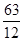 = 5,3;
= 5,3; 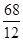 = 5,7;
= 5,7; 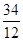 = 2,8;
= 2,8; 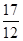 = 1,4, тобто на кожного робочого 2 розряду доводиться в 4 рази менше робочих 1 розряду, 5 робочих 3 розряду; 6 робочих 4 розряду і т.д.
= 1,4, тобто на кожного робочого 2 розряду доводиться в 4 рази менше робочих 1 розряду, 5 робочих 3 розряду; 6 робочих 4 розряду і т.д.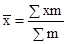 ;
;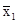 =
= 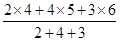 =
= 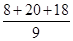 = 5 розряд.
= 5 розряд.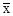 =
= 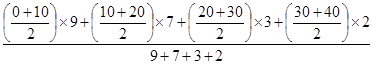 =
= 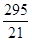 = 14 років.
= 14 років.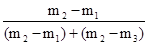 ∙ (x 1 - x 0),
∙ (x 1 - x 0),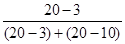 '(105 - 100) = 103,1%.
'(105 - 100) = 103,1%.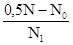 ∙ (x 1 - x 0),
∙ (x 1 - x 0),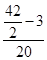 '5 = 104,5%.
'5 = 104,5%.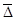 ) Визначається на основі даних абсолютних приростів за такою формулою:
) Визначається на основі даних абсолютних приростів за такою формулою: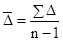 або
або 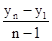 ,
,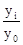 '100%,
'100%,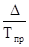 .
.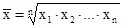 ∙ 100
∙ 100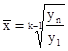 ∙ 100,
∙ 100,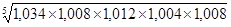 =
= 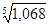 = 1,014 '100 = 101,4% або
= 1,014 '100 = 101,4% або 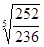 =
= 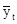 = 18,6 + 0,09t
= 18,6 + 0,09t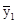 =
= 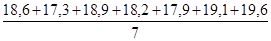 = 18,5;
= 18,5;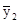 =
= 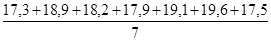 = 18,4 і т.д.
= 18,4 і т.д.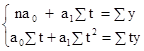 ,
,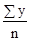 =
= 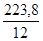 = 18,6;
= 18,6;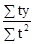 =
= 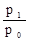 = 0,09.
= 0,09.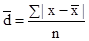 ,
,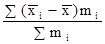 ,
,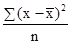 .
.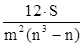 .
.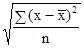 ,
,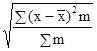 .
.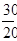 '100%.
'100%.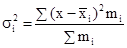
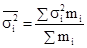 ,
,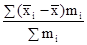 .
.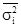 + Γ 2.
+ Γ 2.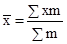 =
= 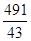 = 11,4 року
= 11,4 року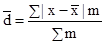 =
= 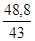 = 1,1 року.
= 1,1 року.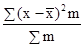 =
= 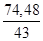 = 1,73;
= 1,73;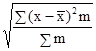 =
= 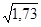 = 1,3 року.
= 1,3 року.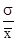 '100 =
'100 = 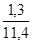 '100 = 11,4%.
'100 = 11,4%.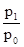 ; I t =
; I t = 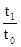 ; I q =
; I q = 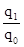 і т.д.,
і т.д.,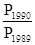 ;
; 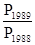 ;
; 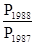 і т.д.
і т.д.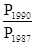 =
= 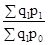 ;
;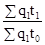 ;
;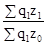 ;
;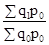 (При наявності соизмерителя p);
(При наявності соизмерителя p);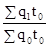 (При наявності соизмерителя t);
(При наявності соизмерителя t);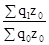 (При наявності соизмерителя z).
(При наявності соизмерителя z).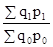 ; індекс витрат праці на виробництво продукції J qt =
; індекс витрат праці на виробництво продукції J qt = 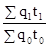 ; індекс грошових витрат на виробництво продукції J qz =
; індекс грошових витрат на виробництво продукції J qz = 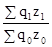 .
.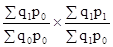 ;
;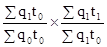 ;
;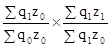 .
.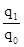 =
= 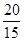 '100 = 133,3%;
'100 = 133,3%;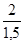 '100 = 133,3%;
'100 = 133,3%;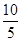 '100 = 200%.
'100 = 200%.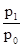 =
= 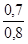 '100 = 87,5%;
'100 = 87,5%;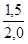 '100 = 75,0%;
'100 = 75,0%;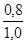 '100 = 80,0%.
'100 = 80,0%.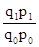 =
= 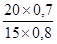 '100 =
'100 = 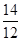 '100 = 116,7%;
'100 = 116,7%;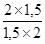 '100 =
'100 = 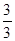 '100 = 100%;
'100 = 100%;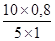 '100 =
'100 = 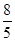 '100 = 160%.
'100 = 160%.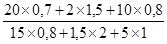 '100 =
'100 = 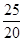 '100 = 125%;
'100 = 125%;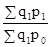 =
=  '100 =
'100 = 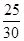 '100 = 83,3%;
'100 = 83,3%;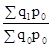 =
= 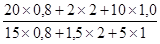 '100 =
'100 = 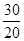 '100 = 150%.
'100 = 150%.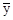 і провівши розрахунки, отримуємо:
і провівши розрахунки, отримуємо: 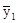 = 14,0;
= 14,0; 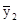 = 16,79;
= 16,79; 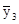 = 22,51;
= 22,51; 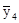 = 24,67;
= 24,67; 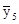 = 32,65;
= 32,65; 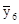 = 36,88;
= 36,88; 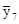 = 41,79.
= 41,79.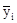 ) Називається емпіричною лінією регресії.
) Називається емпіричною лінією регресії.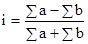 .
.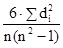 ,
,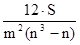 ,
,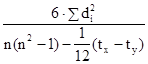 ;
;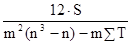 ,
,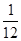 (t 3 - t), а t - кількість зв'язкових рангів за окремими показниками.
(t 3 - t), а t - кількість зв'язкових рангів за окремими показниками.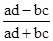 - асоціації;
- асоціації;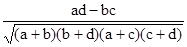 - контингенции.
- контингенции.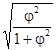 ,
,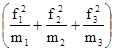 : N 1 = L 1;
: N 1 = L 1;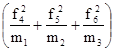 : N 2 = L 2;
: N 2 = L 2;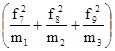 : N 3 = L 3;
: N 3 = L 3;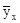 = A 0 + a 1 x;
= A 0 + a 1 x;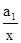 ;
;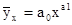 .
.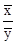 .
.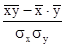 ,
,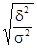 .
.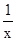 = Σy;
= Σy;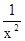 = Σy
= Σy 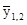 = A 0 + a 1 x + a 2 z,
= A 0 + a 1 x + a 2 z,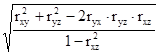 ,
,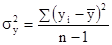 ;
;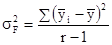 ;
;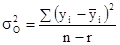 ,
,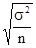 =
= 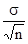 ,
,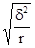 =
= 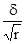 ,
,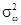 = W (1 - w) замість
= W (1 - w) замість 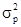 = Pq.
= Pq.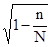 <1 або K =
<1 або K = 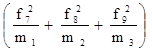 =
=