Методичні вказівки по курсу Математика для студентів I курсу історичного факультету
|
Скачати 54.91 Kb.
|
|
| Дата конвертації | 01.02.2018 |
| Розмір | 54.91 Kb. |
| Тип | реферат |
|
|
-
Навігація по даній сторінці:
- Викладач Попова Н.А.
- Залік ставиться з урахуванням оцінок за
- Список основної літератури
- Додаток 1.
- Завдання 1. (Безліч. Комбінаторика.)
- Завдання 3 (Теорія ймовірностей)
- Завдання 4 (Математична логіка).
- Приклади.
- Додаток 2.
- Додаток 3.
|
Сиктивкарський державний університет Кафедра математичного аналізу Методичні вказівки з курсу "Математика" для студентів I курсу історичного факультету (заочне відділення) Викладач Попова Н.А. Сиктивкар 2001 Навчальний план з курсу "Математика" для I курсу історичного факультету (заочне відділення) на 2001-02 н.р. викладача Попової Н.А. I семестр. Лекції (4 години) 1. Короткий історичний нарис розвитку математики. Огляд літератури. 2. Безліч, елементи комбінаторики, введення в теорію ймовірностей і математичну логіку, знайомство з графами. Консультація (1 година). Методичні вказівки до виконання контрольної роботи. Завдання для самостійної роботи: 1. Контрольна робота (5 завдань. Див. Додаток 1). 2. Підготовка (написання) реферату з обраної теми (список тем - додаток 2). II семестр. Практичні заняття (12 годин). Вирішення задач. 1. Множини. Елементи комбінаторики. 2. Елементи теорії графів і математичної логіки. 3. Елементи теорії ймовірностей. Математичне сподівання і дисперсія, їх застосування в математичній статистиці. 4. Функції та їх графіки. Семінари. 5-6. Деякі питання історії розвитку математики (основні віхи розвитку суспільства і розвитку математики). Консультації (до заліку) - 13 годин. Залік ставиться з урахуванням оцінок за: 2) реферат (за індивідуальною темою), 3) участь у роботі практичних занять (загальна оцінка за 6 занять), 4) відповіді на питання заліку по двох частинах (2 питання, додаток 3). Список основної літератури: 1. Ловягин Ю.М., Матвєєва О.П. Математика. Навчальний посібник для студентів нематематичних спеціальностей. Ч.1. Диференціальне й інтегральне числення. Сикт-р. СГУ, 1998. 73 с. Ч.2. Теорія імовірності. Графи. СГУ, 1999. 64 с. 2. Матвєєв І.В. Функції та їх графіки. М. МГУ, 1970. 104 с. 3. Столл Р.Р. Безлічі. Логіка. Аксіоматичні теорії. М. Просвіта., 1968. 230 с. 4. Крамор В.С. Повторюємо і систематизуємо шкільний курс алгебри і початків аналізу. М. Просвещение, 1990. 416 с. 5. Шіхановіч Ю.А. Введення в сучасну математику (Початкові поняття). М. Наука, 1965. 376 с. 6. Головач П.А. Введення в теорію графів. Сиктивкар. СГУ, 1993. 7. Гнеденко Б.В., Хинчин А.Я. Введення в теорію ймовірностей. М. Физматгиз, 1982. 160 с. 8. Колмогоров А.Н., Журбенко І.Т., Прохоров А.В. Введення в теорію ймовірностей. М. Физматгиз, 1982. 9. Мендельсон Е. Введення в математичну логіку. М. Наука, 1984. 320 с. 10. Валуце І.І., Ділігул Г.Д. Математика для технікумів. Навчальний посібник. М. Наука, 1989. 576 с. 11. Стройк Д.Я. Короткий нарис історії математики. М. Наука, 1978. 336 с. 12. Рибников К.А. Виникнення і розвиток математичної науки. Посібник для вчителя. М. Просвещение, 1987. 159 с. Додаток 1. Контрольна робота з математики для I курсу історичного факультету СГУ (заочне відділення) Завдання 1. (Безліч. Комбінаторика.) 1) Скласти безлічі різних букв. А - свого повного імені, В - свого по батькові, С - свого прізвища. 2) Знайти об'єднання і перетин множин А і В. 3) Знайти доповнення до С до А і до А до С. 4) Перевірити на діаграмах, чи вірно рівність: 5) Обчислити, скільки елементів має декартовій твір множин А і В, зобразити їх точками площини. 6) Скільки різних абревіатур можна скласти з усіх букв безлічі С? У кожній з абревіатур використовувати кожну букву з безлічі С тільки по одному разу (тобто без повторень). 7) Скільки різних трибуквених слів можна скласти з букв безлічі В, якщо слова складаються з різних букв (без повторень)? Що собою являють набори букв цих слів - поєднання або розміщення? 8) Скільки різних підмножин (всіх) має безліч А? Приклад вирішення такого завдання. Нехай автор - Пафнутій Львович Чебишев (будемо вважати е і е за одну і ту ж букву). тоді 1) А = {П, А, Ф, Н, У, Т, І, Й}, В = {Л, Ь, В, О, І, Ч}, С = {Ч, Е, Б, И, Ш , В}. 2) 3) Оскільки 4)
Відповідь: Оскільки вийшло одне і те ж безліч, то рівність вірно.
І
П А Ф Н У Т І Й 6) Так як абревіатури складаються з усіх букв безлічі С і без повторень, то їх кількість дорівнює безлічі порядків на безлічі З: 7) Оскільки при перестановці букв в слові виходять інші (нові) слова (наприклад, ЛОВ і ВІЛ), то набори букв для слів - це розміщення, тому що важливий порядок вибору букв. Всіх розміщень з букв безлічі В по 3 - Відповідь: 100. 8) Оскільки Завдання 2 (Графи) Нехай безліч А з попереднього завдання є безліч позначень вершин для побудови графів, тобто безлічі точок V. 1) 2) Знайти серед зображених графів а) ейлерів граф, б) полуейлеров граф, в) граф, який має цикли (якщо вони є на малюнках, підписати їх, якщо ні, то зобразити такі графи). 3) З множин А, В і С попереднього завдання вибрати безліч з найменшим числом літер (елементів) і, вважаючи їх вершинами графа, зобразити всі можливі дерева з вершинами у всіх цих точках. Наприклад.
ac повний граф з п'ятьма вершинами; він же регулярний
ld однозв'язний.
l
s
xv
y Завдання 3 (Теорія ймовірностей) Візьмемо безлічі А і В з завдання 1. Нехай кожна з букв написана на окремій картці і безлічі А і В - це дві колоди карток (всі картки покладені літерами вниз, їх не видно). Обчислити ймовірність того, що при виборі навмання по одній картці з кожної колоди будуть вийняті а) 2 однакові букви; б) 2 різні літери; в) хоча б одна з букв така, яку Ви задумали заздалегідь (вкажіть, яку саме; якщо є різні варіанти вирішення, то покажіть всі рішення). Наприклад,) А = {П, А, Ф, Н, У, Т, І, Й}, В = {Л, Ь, В, О, В, І, Ч}. Тоді: а) загальна буква тільки одна - І; ймовірність її вибору з А дорівнює Увага! У завданнях 4 і 5 кожен студент повинен виконати свій варіант. Номер варіанту відповідає Вашим номером залікової книжки наступним чином: а) якщо дві останні цифри номера залікової книжки становлять число не більше тридцяти, то це і є номер Вашого варіанту; б) якщо дві останні цифри становлять число більше тридцяти, то з нього слід відняти 30 стільки разів, скільки можливо; залишок і є номер Вашого варіанту; якщо дві останні цифри номера залікової книжки 60 чи 90, то Ви виконуєте варіант 30. Наприклад, номер залікової книжки ... 41 - варіант 11, тому що 41 = 30 + 11, ... 62 - варіант 2, ... 97 - варіант 7; ... 208 - тобто ... 08 - варіант 8. Завдання 4 (Математична логіка). А. У варіантах 1 - 15 скласти таблицю істинності формули: 1. ù x & y Ú (ù y º x Úù y); 2. ù (x & ù y) Ú (ù x & y) ºù y); 3. y Úù x & (y & x ®ù x); 4. x Ú y º (ù x & ù y ® y); 5. x º (x Úù y ®ù y & ù x); 6. (y ®ù x Ú (x & y)) º x Ú y; 7. ù (x Úù y) ® (x Úù y); 8. x Ú (y ® y Úù (x Ú y)); 9. x Ú y ®ù y & (x ® y); 10. x & (ù y ® x Ú y); 11. x º (y ®ù x Ú (x ºù y)); 12. (x Ú y) ® (y & ù x); 13. (x ® y) ® (ù x & ù (y Ú x)); 14. x º (ù y ® x) Ú (x ®ù y)); 15. (x Úù y) & (ù x Ú y) ºù y; Б. У варіантах 16-30 перевірити, чи є формула тавтологією: 16. (y ® (x Úù y)) & (x ® (y Úù x)); 17. (x Ú y) ® (y Úù x); 18. x º (x Úù y) & ù y); 19. x ® (x Ú (ù y & x)); 20. x ® ((y & ù x) ® x); 21. (x ® y) ® x Ú y ºù (ù x & ù y); 22. x Ú y ºù (ù x & ù y); 23. (ù x Ú y ® y) º x Ú y; 24. (ù x Ú y ® x) º x & y; 25. ù (x ® y) Ú (ù y ®ù x); 26. ù (x ® y) & ù (y ®ù x); 27. x & ù y ® (x Ú y ºù x); 28. x Úù y ® (ù y & ù x) ºù x; 29. x º (y ® x & ù y); 30. ù x º (y Ú (x ®ù y)). Приклади. А. Скласти таблицю істинності формули (X ®ù y) & (x Ú y)) º x Úù y. Рішення. Порядок виконання дій: x ® t
Б.Перевірити, чи є формула (x ®ù y) & (x Ú y)) º (x ®ù y) тавтологією. Рішення (аналогічно рішенням попередньої задачі, відрізняється лише v: x ®ù y.
Відповідь: так, тавтологія. Завдання 5. Побудувати графік дрібно-раціональної функції 1) знайти область визначення функції 2) якщо є точки розриву, то з'ясувати, чи є в них вертикальні асимптоти (для цього знайти в цих точках межі функції зліва і справа); 3) знайти похилі або горизонтальні асимптоти (для цього перетворити формулу функції, виділивши цілу частину з дробу); 4) перевірити, чи не володіє функція приватними властивостями: а) парність або непарність, б) періодичністю (якщо немає, то довести, пояснити це); 5) знайти точки перетину графіка з осями координат і інтервали знакопостоянства, якщо точки перетину з віссю 6) знайти похідну і критичні точки; 7) за знаком похідної з'ясувати інтервали зростання і спадання функції і що вона має в критичних точках; 8) зобразити систему координат (відповідно до дослідженими властивостями) і зазначити в ній всі знайдені точки, зобразити асимптоти; для уточнення виду графіка знайти координати декількох додаткових точок; відзначити їх і намалювати графік; 9) якщо в п.5 не були знайдені точки перетину графіка з віссю 10) знайти область зміни функції (за графіком і дослідженим властивостями). варіанти: 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) Приклад. дослідити функцію Рішення. 1) значить, 2) а) при
при
значить, б) при
асимптоти немає; 3) В
4) Досліджуємо на парність:
5) а) при
б)
З урахуванням точок розриву і знайдених значень функції (по (1), (2), (3) і (4), (5)) отримуємо: при при 6) (Використана формула: а) немає критичних точок, де ня тільки при б) значить,
7)
Оскільки при
8)
9) см. 5). 10) 5 y
-2
-12
-38
-40 Додаток 2. теми рефератів 1. Виникнення поняття числа; перші системи числення. 2. Математика в Стародавньому Єгипті. 3. Математика в Древній Месопотамії (Шумер, Вавилон, Ассирія). 4. Математика в Стародавньому Китаї. 5. Математика в Древній Греції (1 тисячоліття до н.е.). 6. Піфагор. *) 7. Аристотель. 8. Евклід. 9. Архімед. 10. Математика Стародавньої Греції та Стародавнього Риму (початок нової ери - IV століття; Олександрійська школа). 11. Середньовіччя. Математика в Індії. 12. Математика в Середній Азії (VIII-XIII століття, Улугбек, Омар Хайям і ін.). 13. Математика в древньої Русі (VIII-XIII століття). 14. Математика в епоху Відродження (Західна Європа; XII-XV століття). 15. Леонардо Пізанський (Фібоначчі). XV століття. 16. Леонардо да Вінчі. XV століття. 17. Франсуа Вієт. XVI століття. 18. Джон Непер (Непер). XVI століття. 19. Кардано і Тарталья. XVI століття. 20. Коперник, Тихо Браге, Кеплер, Галілей. XVI століття. 21. Рене Декарт. XVII століття. 22. Блез Паскаль. XVII століття. 23. Ісаак Ньютон. XVII століття. 24. Г. В. Лейбніц. XVII століття. 25. П'єр Ферма. XVII століття. 26. Даламбер. XVIII століття. 27. Леонард Ейлер. XVIII століття. 28. Ж.Л.Лагранж. XVIII століття. 29. А.М.Лежандр. XVIII століття. 30. Г.Монж. XVIII століття. 31. П.С.Лаплас. XVIII століття. 32. Математика в Росії XVII-XVIII століть (Роль реформ Петра I; Катерина II). 33. М. В. Ломоносов. 34. Знамениті завдання давнини (про подвоєння куба, про трисекции кута, про випрямлення окружності) і їх дозвіл (аж до XVIII століття). 35. К.Ф.Гаусс. 36. Різні докази V постулату Евкліда (до XIX ст. Н.е.). 37. Н.И.Лобачевский 38. Основні початкові факти геометрії Лобачевського, моделі площині Лобачевського. 39. Нільс Абель. XIX століття. 40. Еваріст Галуа. XIX століття. 41. Огюстен Коші. XIX століття. 42. Карл Вейерштрасс. XIX століття. 43. М. В. Остроградський. XIX століття. 44. П.Л.Чебишёв. XIX століття. 45. С.В.Ковалевская. XIX століття. 46. Ф.Клейна. XIX століття. 47. А. Пуанкаре. XIX століття. 48. Г. Кантора. XIX століття. 49. Б.Ріман. Кінець XIX століття. 50. Д. Гільберт. Кінець XIX століття. 51. Французька математична школа (XVII-XX ст). 52. Німецька математична школа (XVII-XX ст). 53. Англійська математична школа (XVII-XX ст). 54. Російська математична школа (XVIII-началоXX ст.ст.). 55. Радянська математична школа. 56. Американська математична школа (XIX-X X ст.ст.). 57. Н. Вінер. 58. А.Н.Колмогоров. 59. Математика XX століття; основні напрямки розвитку. 60. Основні стадії розвитку науки; основні риси сучасної математики і її роль у розвитку суспільства. Примітка. Додаткова література до роботи над рефератом не вказана, тому що підбір літератури входить як частина в самостійну роботу студента (цього треба навчитися). У посібнику Д.Я.Стройка [11] в кінці кожного розділу є список рекомендованої літератури. Можна використовувати те, що знайдеться в особистій бібліотеці або в найближчій громадської, в т.ч. і статті з журналів "Квант", "Математика в школі" та інших періодичних видань, а також енциклопедичні словники. Додаток 3. Питання до заліку з курсу "Математика" для студентів I курсу історичного факультету СГУ Частина 1. Математика. 1. Поняття множини; елементи множини; потужність безлічі; відносини власності і включення. Види множин. 2. Числові множини. 3. Операції над множинами, їх властивості. 4. Відповідності між елементами множин, їх види (в т.ч. відображення і біекція). 5. Функції, їх дослідження. 6. Поняття графа. Види графів, їх застосування. 7. Поняття про комбінаторної задачі. Правила суми і твори. 8. Порядок на безлічі. Кількість всіх порядків безлічі потужності 9. Підмножини з 10. Впорядковані підмножини з 11. Властивості сполучень, їх застосування. 12. Випадкові події. Достовірні і неможливі події. Випробування, елементарний результат, повна система результатів. Відносна частота і ймовірність спостережуваного події. 13. Спільні і несумісні, залежні і незалежні події. Правила суми і твори. 14. Випадкові величини. Функція розподілу випадкових величин. Математичне очікування. 15. Дисперсія. Закон великих чисел. 16. Висловлювання; висказивательной форми; квантори спільності та існування. Область відправлення і безліч істинності висловлювання. 17. Логічні операції над висловлюваннями (логічні зв'язки), порядок їх виконання в складній формулі. 18. Заперечення логічних зв'язок. 19. Властивості диз'юнкції і кон'юнкції. 20. Властивості імплікації і еквівалентності. Частина 2. Історія математики. 1. Етапи розвитку науки; роль математики в розвитку наук і особливості її розвитку. 2. Виникнення основних математичних понять (число, фігура, ...). 3. Позначення чисел і системи числення у різних народів. 4. Математика в древніх Месопотамії та Єгипті. Математика в древніх Китаї та Індії. 5. Математика в Древній Греції і Древньому Римі. 6. Математика в Середні віки (Середня Азія). 7. Математика в древньої Русі. 8. Математика середньовіччя в Західній Європі. 9. Математика Епохи Відродження. 10. Математика Західної Європи в XVII столітті. 11. Математика в Росії в XIV-XVII ст. (Вплив татаро-монгольського ярма і відносин із Західною Європою). 12. Розвиток математики в XVIII столітті в Західній Європі. 13. Те ж - в Росії. 14. Виникнення диференціального й інтегрального числення; їх розвиток. 15. Геометрія - XIX століття. 16. 23 проблеми, поставлені Гильбертом, їх рішення. 17. Основні гілки математики, їх зародження і роль в даний час (алгебра, теорія чисел, теорія ймовірностей, тригонометрія, ...). 18. Кібернетика і інформатика. 19. Підстави математики і математична логіка. 20. Основні риси сучасної математики і шляхи її розвитку. Вересень 2001 року Н.А.Попова *) Тут і далі ім'я вченого означає, що потрібно викласти відомості про його життя і його внесок в історію розвитку математики. |
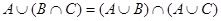 .
.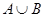 = {П, А, Ф, Н, У, Т, І, Й, Л, Ь, В, О, Ч}.
= {П, А, Ф, Н, У, Т, І, Й, Л, Ь, В, О, Ч}. 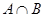 = {І}.
= {І}.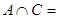 Æ, то
Æ, то 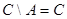 і
і 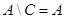 .
.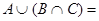 {П, А, Ф, Н, У, Т, І, Й, У, Ч}.
{П, А, Ф, Н, У, Т, І, Й, У, Ч}.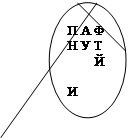














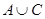

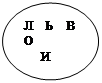
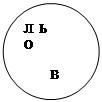
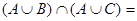 {П, А, Ф, Н, У, Т, І, Й, У, Ч}.
{П, А, Ф, Н, У, Т, І, Й, У, Ч}.

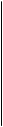 5)
5) 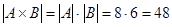 . Ч
. Ч Про
Про В
В
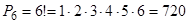 .
.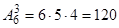 .Але немає слів, що починаються з літери "ь", тому такі набори треба виключити,
.Але немає слів, що починаються з літери "ь", тому такі набори треба виключити, 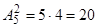 . Тоді різних трибуквених слів
. Тоді різних трибуквених слів 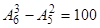 .
.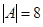 , То кількість підмножин -
, То кількість підмножин - 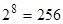 .
. Зобразити вершини графа точками, позначити їх і з'єднати ребрами так, щоб вийшов а) повний граф -
Зобразити вершини графа точками, позначити їх і з'єднати ребрами так, щоб вийшов а) повний граф - 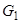 , Б) двочастковий граф -
, Б) двочастковий граф - 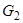 , В)
, В) 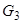 , Г) регулярний граф -
, Г) регулярний граф - 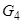 (Вказати його ступінь), д) однозв'язний граф з одним "мостом" -
(Вказати його ступінь), д) однозв'язний граф з одним "мостом" - 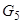 , Е) непростий граф -
, Е) непростий граф - 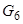 (Тобто виконати не менше шести малюнків).
(Тобто виконати не менше шести малюнків).


 b
b




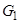
 (Однорідний), ступінь вершин r = 4; а також він Ейлером;
(Однорідний), ступінь вершин r = 4; а також він Ейлером;
 m неповний).
m неповний).
 ko
ko
 pq
pq



 полуейлеров граф.
полуейлеров граф.

 zw
zw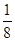 , Ймовірність її вибору з В дорівнює
, Ймовірність її вибору з В дорівнює 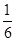 ; ймовірність її вибору з А і з В -
; ймовірність її вибору з А і з В - 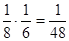 (Правило твори); б) тому що у всіх інших випадках букви будуть різні, то ймовірність вибору двох різних букв дорівнює
(Правило твори); б) тому що у всіх інших випадках букви будуть різні, то ймовірність вибору двох різних букв дорівнює 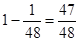 (Можна її знайти і іншим способом); в) якщо задумана буква "І", то ймовірність її вибору хоча б з однієї колоди - це 3 випадки: "І"
(Можна її знайти і іншим способом); в) якщо задумана буква "І", то ймовірність її вибору хоча б з однієї колоди - це 3 випадки: "І" 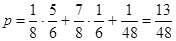 Аналогічно для інших букв (2 вип.).
Аналогічно для інших букв (2 вип.).
 Ú
Ú
 & Z º
& Z º
 y ùÚ v
y ùÚ v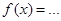 (Варіанти 1-30), попередньо дослідивши її за таким планом:
(Варіанти 1-30), попередньо дослідивши її за таким планом: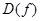 (Для цього можна перетворити формулу, розклавши чисельник і знаменник на множники);
(Для цього можна перетворити формулу, розклавши чисельник і знаменник на множники);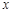 легко знаходяться;
легко знаходяться;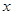 (Нулі функції), то знайти їх тепер за графіком;
(Нулі функції), то знайти їх тепер за графіком;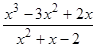 ; 11)
; 11) 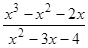 ; 21)
; 21) 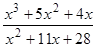 ;
;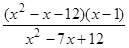 ; 12)
; 12) 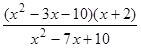 ; 22)
; 22) 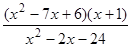 ;
;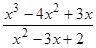 ; 13)
; 13) 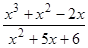 ; 23)
; 23) 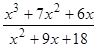 ;
;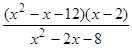 ; 14)
; 14) 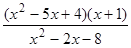 ; 24)
; 24) 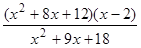 ;
;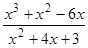 ; 15)
; 15) 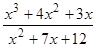 ; 25)
; 25) 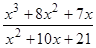 ;
;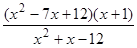 ; 16)
; 16) 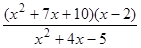 ; 26)
; 26) 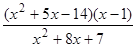 ;
;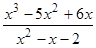 ; 17)
; 17) 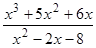 ; 27)
; 27) 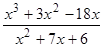 ;
;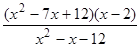 ; 18)
; 18) 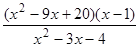 ; 28)
; 28) 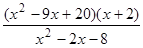 ;
;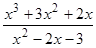 ; 19)
; 19) 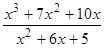 ; 29)
; 29) 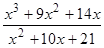 ;
;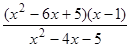 ; 20)
; 20) 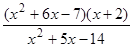 ; 30)
; 30) 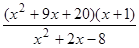 .
.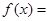
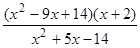 .
. =
= 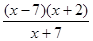 при
при 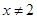 (Коріння квадратного тричлена знайдені по зворотної теоремі Вієта (в умі)),
(Коріння квадратного тричлена знайдені по зворотної теоремі Вієта (в умі)),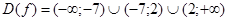 .
.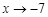 зліва
зліва 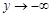 ; (1)
; (1)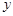
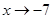
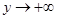 ; (2)
; (2)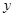
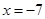 - вертикальна асимптота;
- вертикальна асимптота;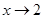 (І зліва і справа)
(І зліва і справа) 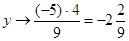 ;
;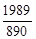
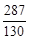
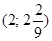 - виключена точка (т. Розриву). (3)
- виключена точка (т. Розриву). (3)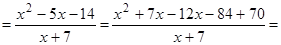
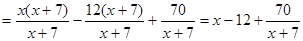 ; тому при
; тому при 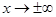
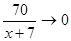 , то
, то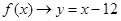 ; таким чином, пряма
; таким чином, пряма 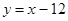 - похила асимптота.
- похила асимптота.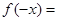
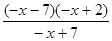
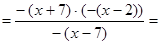
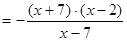 ; бачимо, що:
; бачимо, що: 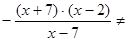
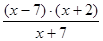 і
і 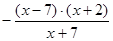 , Т.е.
, Т.е. 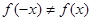 і
і 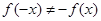 , Значить,
, Значить, 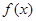 загального вигляду (не володіє ні парністю, ні непарною);
загального вигляду (не володіє ні парністю, ні непарною); 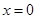
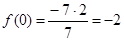 ; значить,
; значить,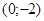 - точка перетину графіка з віссю ординат; (4)
- точка перетину графіка з віссю ординат; (4)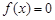 при
при 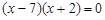 , але
, але 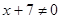 ,
, 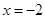 або
або 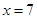 , Таким чином
, Таким чином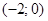 і
і 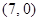 - точки перетину графіка
- точки перетину графіка 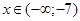
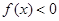 ; при
; при 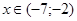
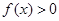 ;
;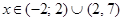
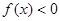 ; при
; при 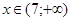
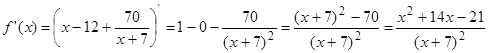
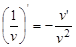 );
);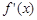 не існує, тому що
не існує, тому що 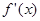 не має значен
не має значен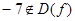 ;
;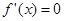 при
при 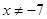 і
і 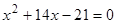 , Тобто при
, Тобто при 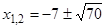 ;
; 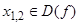 ;
;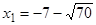 і
і 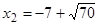 - критичні точки, а
- критичні точки, а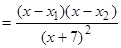 ;
; 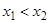 .
.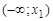
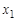
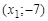
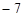
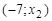
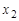
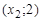
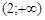




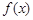

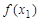
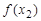
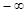 до
до 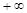
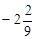
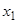 і
і 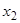
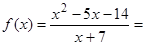
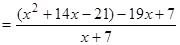 ; тоді
; тоді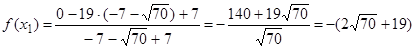 ;
; 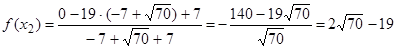 ;
;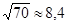 ; тому
; тому 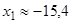 ,
, 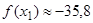 ;
; 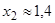 ,
, 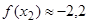 .
.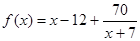 ;
;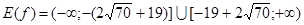 .
.



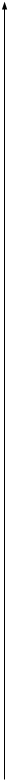


 -21 -17 -14 -12 -7 -2 0 7 12 x
-21 -17 -14 -12 -7 -2 0 7 12 x




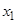
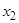
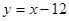
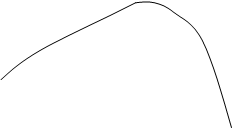
 -36
-36
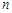 . перестановки з
. перестановки з 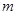 . Сполучення. Кількість всіх підмножин множини,
. Сполучення. Кількість всіх підмножин множини, 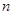 по
по