Завдання а: Ввести поняття «золотий перетин» (трохи про історію). Алгебраїчне знаходження «золотого перетину», геометричне побудова «золотого перетину». Розглянути застосування «золотого перетину» в
|
Скачати 23.73 Kb.
|
|
| Дата конвертації | 15.06.2019 |
| Розмір | 23.73 Kb. |
| Тип | реферат |
|
|
-
Навігація по даній сторінці:
- «ЗОЛОТИЙ ПЕРЕТИН» І ЗАКОНИ МИСТЕЦТВА В Стародавньої Греції.
- Статуя «Дорифор».
- Пентаграма представляє собою вмістилище «золотих пропорцій».
- «Золота пропорція» і повязані з нею відносини.
- «Золотий перетин» і «золота спіраль» в живій природі
- Застосування «золотого перетину» в архітектурі міст
- Будівля Новокузнецкого драматичного театру.
|
«Середня загальноосвітня школа №92» X шкільна науково-практична конференція Золотий перетин виконала: учениця 9а класу Дороднева Анастасія керівник: вчитель математики Прокопенко О.І. Новокузнецьк, 2007р. Зміст. 1. Введення ----------------------------------------------- -------------------- 3 2. Дещо з історії .-------------------------------------------- --------- 4 3. «Золотий перетин» і закони мистецтва в Стародавній Греції .---- 7 4. «Золотое сечение» і «золота спіраль в живій природі» .---- 12 5. Застосування «золотого перетину» в архітектурі міст .------ 12 7. Висновок .---------------------------------------------- ---------------- 14 8. Список літератури .--------------------------------------------- ------- 17 Вступ. Метою реферату є наступне: скориставшись різноманітною літературою по геометрії, з креслення, різними довідковими матеріалами для більш докладного вивчення теми «Золотое сечение», дати найбільш повне уявлення про цю тему; розглянути застосування «золотого перетину». Завдання реферату: 1. Ввести поняття «золотий перетин» (трохи про історію). Алгебраїчне знаходження «золотого перетину», геометричне побудова «золотого перетину». 2. Розглянути застосування «золотого перетину» в мистецтві Стародавньої Греції. 3. Розглянемо золоту пропорцію і пов'язані з нею відносини. 4. Продемонструвати і розібрати поняття золотий спіралі в живій природі. 5. Показати застосування «золотого перетину» в епоху Відродження. 6. Частково вивчивши архітектуру міст, вказати найбільш відомі будівлі з застосуванням золотого перетину. Я зайнялася детальним вивченням теми «Золотое сечение» після того, як одного разу на уроках геометрії почула про широке застосування «золотого перетину» в архітектурі. Я розглянула різні енциклопедичні відомості, розробки вчених, що займалися темою «Золотое сечение». Для знаходження матеріалу для мого проекту використовувала енциклопедичні довідники з математики, підручники з архітектури, навчальні посібники. Трішки історії... «Золотий перетин» поділу в крайньому і середньому відношенні - поділ відрізка АВ на дві частини таким чином, що більша частина АС є середньою пропорційною між усім відрізком АВ і меншою його частиною СВ. Алгебраїчне побудова «золотого перетину» АВ = а зводиться до вирішення рівняння а: х = х: (а - х) (де х = АС), звідки х = Ставлення х до а може бути виражено наближено дробом АВ: АС = АС: СВ (рис. 1).
У дійшла до нас античній літературі «золотий перетин» вперше зустрічається в II книзі «Начал» Евкліда, де дається його геометричну побудову, рівносильне рішенню квадратного рівняння виду х (а + х) = = а 2. Евклід застосовував «золотий перетин» при побудові правильних 5- і 10-кутників, а також в стереометрії при побудові правильних 12- і 20-гранником. Безсумнівно, що «золотий перетин» було відомо і до Евкліда. Досить імовірно, що завдання «золотого перетину» була вирішена ще піфагорійцями, яким приписуються побудова правильного 5-кутника і геометричної побудови, рівносильні рішенням квадратних рівнянь. Саме пентаграму Піфагорійці вибрали символом свого союзу - релігійної секти на чолі з Піфагором (бл. 580-500 до н. Е.), Яка проповідувала братню любов один до одного, зречення від зовнішнього світу, спільність майна і т. Д. Піфагорійців відрізняло від інших то, що вони вважали можливим домогтися очищення духу за допомогою математики. За їх теорії, в основу світового порядку покладено числа. Світ, вважали вони, складається з протилежностей до єдності. Гармонія ж полягає в числових відносинах. Піфагорійці приписували числам різні властивості. Так, парні числа вони називали жіночими, непарні (крім 1) - чоловічими. Число 5 - як сума першого жіночого числа (2) і першого чоловічого (3) - вважалося символом любові. Звідси така увага до пентаграмме, що має 5 кутів. Після Евкліда дослідженням «золотого перетину» займалися Гипсикл (II ст. До н. Е.), Папп Олександрійський (III в. Н. Е.) Та ін. У середньовічній Європі з «золотим перетином» познайомилися з арабським перекладам «Начал» Евкліда. Перекладач і коментатор Евкліда Дж. Кампано з Новари (XIII в.) Додав до 13 книзі «Начал» припущення, що містить арифметичне доказ неспівмірності відрізка і обох частин його «золотого перетину». У XV-XVI ст. посилився інтерес до «золотого перетину» серед учених і художників "в зв'язку з його застосуванням як у геометрії, так і в мистецтві, особливо в архітектурі. В середні віки вважалося, що пентаграма служить охоронним знаком від сатани. Згадаймо, наприклад, як описує Гете проникнення диявола Мефістофеля в келію доктора Фауста, на якій була написана пентаграма. Мефістофель спочатку покликав чорного пуделя відгризти кінчик двері з частиною пентаграми. Тільки після цього він сам зміг постати перед Фаустом. Л. Пачолі присвятив «золотого перетину» тр актат «Про божественної пропорції» (1509); про «золотий перетин» багато писав в одному зі своїх ранніх творів І. Кеплер (1596). Ленард да Вінчі вважав, що ідеальні пропорції людського тіла повинні бути пов'язані числом Ф, поділ відрізка щодо Ф він назвав «золотим перерізом». «Золотое сечение» або близькі йому пропорційні відносини лягли в основу композиційної побудови багатьох творів світового мистецтва, наприклад, Капела пації у Флоренції, архітектора Ф. Брунеллески, XV в. «ЗОЛОТИЙ ПЕРЕТИН» І ЗАКОНИ МИСТЕЦТВА В Стародавньої Греції.
Статуя «Дорифор».
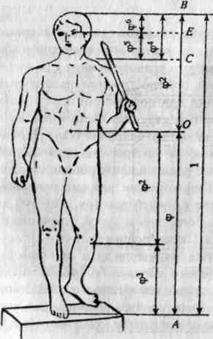
Розглянемо тепер застосування «золотого перетину» в скульптурах Стародавньої Греції. Роботи Фідія в оригіналах майже не збереглися, тому для ілюстрації візьмемо твір його молодшого сучасника, скульптора і теоретика мистецтва Поліклета (друга половина V ст. До н. Е.). У своєму трактаті «Канон» він прагнув встановити закони пропорційності людського тіла. Теорія пропорцій Поліклета яскраво втілилася в статуї «Дорифор» -копьеносец, яку він створив в суворій відповідності всіх частин. У цій статуї ми зустрічаємо багато разів застосоване число. Так, пупок (точка О) ділить висоту статуї щодо «золотого перетину». Значить, якщо висоту АВ прийняти за 1, то АТ = j, але тоді ОВ = 1 - j. Однак на рис. 2 показано, що відстань ОВ береться рівним. Чи немає тут протиріччя? Перевіримо: якщо вважати, що 1 - j = j, то приходимо до рівняння j 2 + j - 1 = 0. Звідки j = Але проаналізуємо інші пропорції знаменитої статуї. Відстань від підошви списника до його коліна одно j 3, висота шиї разом з головою дорівнює j 4, довжина шиї до вуха - j 5, а відстань вуха до верхівки -j 6. Таким чином, в цій статуї ми бачимо геометричну прогресію зі знаменником j: j 2, j 3, j 4, j 5, j 6.
Парферон. «Золотий перетин» багаторазово зустрічається при аналізі геометричних закономірностей Парферона. Це стародавня споруда з його гармонійними пропорціями дарує нам таке ж естетичну насолоду, як і нашим предкам. Багато мистецтвознавці, які прагнули розкрити секрет того могутнього емоційного впливу, яке ця будівля має на глядача, шукали і знаходили в співвідношеннях його частин золоту пропорцію. Відомий цілий ряд пропорцій. Так, прийнявши за ширину торцевого будівлі, можна отримати геометричну прогресію, що складається з восьми членів: відстань між другою і сьомий колонами одно j, між третьою та шостою - j 2, між четвертою і п'ятою - j 4. Аналогічні закономірності ми бачимо і в побудові будівлі по висоті. Об'єднавши їх, отримаємо прогресію: 1, j, j 2, j 3, j 4, j 5. Тут повчально згадати про пропорції людського тіла, зазначених раніше. Порівнюючи, бачимо, що ставлення торцевої довжини будівлі до його висоті дорівнює відношенню людського зросту до довжини нижньої частини тіла: 1 / j. Висота даху Парфенона відноситься до відстані між дахом і капітелями колон, як j 4: j 5, т. Е. Так само, як відрізок ВС відноситься до відрізка ЄС. Ці збіги не випадкові. У своїх архітектурних творіннях давньогрецькі майстри виходили з пропорцій, які бачили в природі, і перш за все в пропорціях людського тіла. Чим же цікавий цей символ з точки зору математики? Побудуємо спочатку правильний п'ятикутник. Це легко зробити за допомогою описаного кола. З її центру треба послідовно відкласти кути з вершиною в центрі кола, рав360 / 5 = 72 0, сторони кутів перетнуть коло в точках А, В, С, D, Е.Поєднавши їх послідовно, отримаємо правильний п'ятикутник. А тепер проведемо в цьому п'ятикутнику все діагоналі. Вони утворюють правильний зірчастий п'ятикутник, т. Е. Знамениту пентаграму (рис. 2).
Цікаво, що сторони пентаграми, перетинаючись, утворюють знову правильний п'ятикутник, в якому перетин діагоналей дає нам нову пентаграму, а в перетині її сторін ми знову бачимо правильний п'ятикутник, відкриває можливість побудови нової пентаграми. І так далі до нескінченності. Пентаграма представляє собою вмістилище «золотих пропорцій». При п = 5 маємо 180 ° × 3: 5 = 108 °. У п'ятикутнику ABCDE, Ð1 = 108 °: 3 = 36 °. Тепер розглянемо пентаграму на рис. 3. З'єднаємо в ній точки К і F. Вище вже зазначалося, що п'ятикутник KLFPM - правильний, т. Е. Кут KLF = 108 °. Тоді Ðl = Ð2 = 36 °. Але кут Е теж дорівнює 36 °. З того що Ð1 = Ð E, випливає, що ЄС паралельна KF, а тоді Δ ВЕР подібний Δ BKF, ЕВ: KB = РВ: FB. (1) Позначимо ЕВ = а і KB = х, перепишемо пропорцію (1) інакше: а: х = х: (ах), або х 2 + ах - а 2 = 0. Ми отримали те ж саме рівняння, рішенням якого є х = Значить, KB: ЕВ = j.
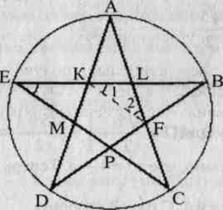 рис.3 рис.3
«Золота пропорція» і пов'язані з нею відносини. Застосування «золотий пропорції» часто зводиться до побудови відрізка довжиною Ф =
Природно поставити питання про те, як побудувати відрізок довжиною Ф.
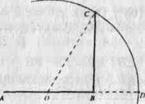
побудова: а) відкладемо відрізок АВ = 1; з точки В відновимо перпендикуляр до відрізка АВ і відкладемо на ньому відрізок ВС = 1; б) розділимо відрізок АВ навпіл точкою О, ОС = в) з точки Про проведемо коло радіусом Раніше було доведено, що j 2 = 1 - j. Тепер доведемо, що Ф 2 = 1 + j Доведення. З одного боку,
З іншого боку, Ф + 1 = «Золотий перетин» і «золота спіраль» в живій природі Краса природних форм народжується у взаємодії двох фізичних сил - тяжіння і інерції. «Золота пропорція» - символ цієї взаємодії, оскільки диктуються нею ставлення більшої частини цілого до самого цілого висловлює основні моменти живого зростання: стрімкий зліт легкого юного втечі до зрілості і сповільнене зростання «за інерцією» до моменту цвітіння, коли досягла повної сили рослина готується дати життя новому побіжу. Одним з перших прояви «золотого перетину» в природі помітив різнобічний спостерігач, автор багатьох сміливих гіпотез німецький математик і астроном Йоганн Кеплер (1571-1630). З XVII ст. спостереження математичних закономірностей в ботаніці і зоології стали швидко накопичуватися. Наведемо один з порівняно недавно встановлених фактів. У 1850 р німецький вчений А. Цейзинг відкрив так званий закон кутів, згідно з яким середня величина кутового відхилення гілки рослини дорівнює приблизно 138 °. Уявімо собі, що дві сусідні гілки рослини виходять з однієї точки (насправді це не так: в реальності гілки розташовуються вище або нижче один від одного). Позначимо одну з них через ОА, іншу через ОВ. Кут між променями-гілками позначимо через a, а кут, що доповнює його до 360 °, - через b. Складемо «золоту пропорцію» ділення до повного кута, вважаючи, що кут В - велика частина цієї величини: 360: b = b: (360- b). Звідси отримуємо рівняння b 2 + 360 b - 360 2 = 0 і знаходимо позитивний корінь b = -180 + Тоді a = 360 ° - 222, 48 ° = 137,52 ° Таким чином, величина середнього кутового відхилення гілки відповідає меншій з двох частин, на які ділиться повний кут при «золотому перетині». Розглянемо тепер розташування насіння в кошику соняшнику. Вони шикуються уздовж спіралей, які закручуються як зліва направо, так і справа наліво. В одну сторону закручено 13 спіралей, в іншу - 21. У більших суцвіттях соняшнику число відповідних спіралей 21 і 34 або 34 і 55. Схоже спіральне розташування спостерігається у лусочок соснових шишок або осередків ананаса. У верхівках дуже багатьох пагонів можна розрізнити такі ж системи спіральних рядів. Число рядів листя або квіток, орієнтованих протилежно, відрізняється у різних рослин, але найчастіше набуває таких значень:
Починаючи з другого члена цього ряду, в ньому повторюється число j, з кожним новим кроком виражається все більш точно: j = = 0,618033 ... Логарифмічна спіраль (рис. 6) єдина з спіралей не змінює своєї форми при збільшенні розмірів. Мабуть, це свій ство
і послужило причиною того, що в живій природі логарифмічна спіраль зустрічається частіше за інших. За логарифмічною спіралі згорнуті раковини багатьох равликів і молюсків; та ж спіраль зустрічається в суцвіттях рослин; навіть павуки, сплітаючи павутини, закручують нитки навколо центра за логарифмічною спіралі. Таким чином, людські уявлення про красивому формуються явно під впливом того, які втілення порядку і гармонії людина бачить в живій природі. А природа, як відомо, любить повторення. У різних своїх творах, здавалося б, дуже далеких один від одного, вона може використовувати одні і ті ж принципи. «Золотий перетин» - один з цих основоположних принципів природи. Застосування «золотого перетину» в архітектурі міст Педагогічний університет міста Волгограда Фасадна частина будівлі педагогічного університету міста Волгограда побудована за принципом «золотого перетину» (рис. 8).
Візьмемо за 1 ширину торцевого фасаду. Відстань між першою і шостою колонами одно j, між другою і п'ятою - j2, між третім і четвертим - jЗ. Аналогічні закономірності ми бачимо і в побудові будівель по висоті. Об'єднавши їх, ми отримуємо прогресію: 1, j, j2, jЗ, j4. Висновок: провівши ряд обчислень і перетворень, я виявила закономірність і визначила, що фасадна частина будівлі педагогічного університету дійсно побудована за принципом «золотого перетину» (рис. 8).
Будівля Новокузнецкого драматичного театру. (Рис.9) рис.8 рис.9
Висновок. Я думаю, що даний реферат є міні-посібником для вивчення «золотого перетину». Можливо, не всі докладно, але в рефераті порушені всі опорно-які вважають аспекти. Також в рефераті розглянуто застосування «золотого перетину» в мистецтві з найдавніших часів до наших днів. Секрет того могутнього емоційного впливу, яке ці будівлі надають на глядача, багато мистецтвознавців шукали і знаходили в співвідношеннях «золотий пропорції». У рефераті описано застосування «золотого перетину» тільки на декількох будівлях, але будівлі, при побудові яких застосовували «золотий перетин», зустрічаються в багатьох містах неодноразово. література 1. Великий енциклопедичний словник: математика. - М .: Велика Російська енциклопедія, 1988. 2. Газета «Математика», додаток до навчально-методичному посібнику «Первое сентября». - Волгоград: видавничий дім «Перше вересня», 2005. 3. Квант: науково-популярна фізико-математична енциклопедія. -М .: Бюро «Квантум». 4. Математичний енциклопедичний словник. - М .: Радянська енциклопедія, 1988. 5. Енциклопедичний словник юного математика. - М .: Педагогіка, 1985. |
- «ЗОЛОТИЙ ПЕРЕТИН» І ЗАКОНИ МИСТЕЦТВА В Стародавньої Греції.
- Статуя «Дорифор».
- Пентаграма представляє собою вмістилище «золотих пропорцій».
- «Золота пропорція» і повязані з нею відносини.
- «Золотий перетин» і «золота спіраль» в живій природі
- Застосування «золотого перетину» в архітектурі міст
- Будівля Новокузнецкого драматичного театру.
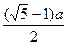 = 0,62а.
= 0,62а. , ..., де 2,3,5,8,13,21, ... - Фібоначчі числа. Геометричну побудову «золотого перетину» відрізка АВ здійснюється так: у точці В відновлюють перпендикуляр до АВ, на ньому відкладають відрізок BE = = \ I 2 AB, з'єднують А і Е, відкладають ED = ЕВ і, нарешті, АС = AD, тоді буде
, ..., де 2,3,5,8,13,21, ... - Фібоначчі числа. Геометричну побудову «золотого перетину» відрізка АВ здійснюється так: у точці В відновлюють перпендикуляр до АВ, на ньому відкладають відрізок BE = = \ I 2 AB, з'єднують А і Е, відкладають ED = ЕВ і, нарешті, АС = AD, тоді буде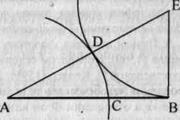
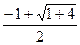 , Т. е. отримали те ж саме значення, яке вирахували раніше.
, Т. е. отримали те ж саме значення, яке вирахували раніше.
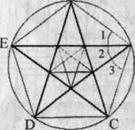 рис.2
рис.2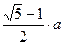
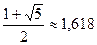 . Це число є зворотним по відношенню до числа j. Справді:
. Це число є зворотним по відношенню до числа j. Справді: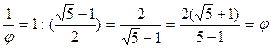
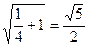
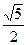 , Що перетинає промінь АВ в точці D, AD =
, Що перетинає промінь АВ в точці D, AD = 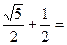 j.
j.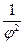 =
= 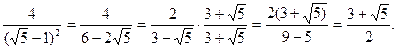
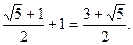 Ф 2 = Ф + 1.
Ф 2 = Ф + 1.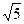 = 222,48.
= 222,48.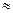 138 °.
138 °.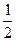 = 0,5;
= 0,5;  = 0,666 ...;
= 0,666 ...;  = 0,6;
= 0,6; 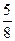 = 0,625 ...,
= 0,625 ..., 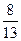 = 0,615 ...,
= 0,615 ..., 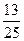 = 0,619047 ...,
= 0,619047 ...,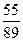 = 0,617977 ...,
= 0,617977 ..., 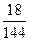 = 0,518055 ...
= 0,518055 ...

