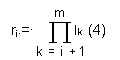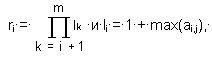|
А.Ф. Оськін, В.І. Шайков
Нинішній етап розвитку історичної науки, як і науки взагалі, характеризується все зростаючим потоком інформації. Обробку великих обсягів інформації за допомогою комп'ютера не можна ефективно організувати тільки шляхом вдосконалення технічних засобів - збільшуючи обсяги пам'яті, скорочуючи час звернення до зовнішніх носіїв і т.д .. Необхідно вдосконалювати також і методи організації інформації, розробляючи ефективні алгоритми її кодування.
Що ж таке інформація? Одне з можливих визначень цього поняття розглядає інформацію як "зміст зв'язку між взаємодіючими матеріальними об'єктами, що виявляється в зміні стану цих об'єктів" [1].
Цікаво відзначити, що в теорії інформації відсутній суворе визначення поняття "інформація". Необхідною і достатньою умовою побудови цієї теорії виявилося запровадження поняття кількості інформації.
Як же визначають кількість інформації? У класичній теорії інформації ігноруються цінність, терміновість і смисловий зміст інформації, тобто не приймаються в розрахунок якісні характеристики повідомлень. Коли ж не враховуються якісні характеристики, то має сенс говорити не про кількість інформації, а про її обсязі. Слід зазначити, що з цієї точки зору історична інформація має ряд особливостей. Для історика досить важливим є завдання створення і збереження в машиночитаемом архіві найбільш повної електронної копії наративного джерела. Якщо врахувати складність і неоднорідність інформації, характерні для історичного джерела, а також швидко збільшується число архівів, що зберігають інформацію у формі,, актуальною стає завдання розробки принципів зберігання інформації. При цьому дуже важливим є пошук шляхів якісного поліпшення методів кодування і зберігання інформації.
Розгляду одного з таких методів і присвячена ця стаття. Надалі під інформацією ми будемо розуміти набори числових даних, оскільки зберігається чином будь-якого джерела може бути число або безліч чисел. При цьому під кількістю інформації ми будемо мати на увазі її обсяг, тобто кількість байтів пам'яті, необхідних для запису елементів числових множин.
Більшість використовуваних в даний час методів кодування грунтується на обліку статистичної інформації про кодованої множині. У роботі В.А. Амелькина [2] наведена одна з можливих класифікацій методів кодування. Відповідно до цієї класифікації, виділяються наступні групи методів:
упаковки (код Бодо);
статистичні методи;
алгоритмічне і комбинаторное кодування.
Методи упаковки.
Як показано в тій же роботі, для кодування множини A, що складається з p елементів, при використанні рівномірного двійкового коду, довжина S кодових повідомлень дорівнює:
S = [log (p)] + 1 (1)
При кодуванні інформації за методом Бодо у вихідній матриці X = відшукується максимальний елемент, для якого відповідно до формули (1)
S o = [log (max (x i, j))] + 1 (2)
розраховується необхідну для його зберігання число двійкових розрядів. При цьому, для зберігання кожного елементу таблиці x i, j відводиться S o двійкових розрядів. Для зберігання всієї таблиці необхідно (n * m * So) двійкових одиниць. (Тут n- число рядків, а m- число стовпців початкової матриці).
Існують модифікації цього методу, що дозволяє підвищити ступінь упаковки. До недоліків методу слід віднести те, що він ефективний лише на матрицях спеціального виду з незначними відмінностями по абсолютним значенням усередині рядка і значного - всередині стовпців (або навпаки).
Статистичні методи.
У цю групу входять методи, засновані на обліку статистичних даних про кодованої множині. Історично першим в цій групі був код Морзе.
У 1948-49 р.р. відразу двома дослідниками Шенноном і Фано незалежно один від одного запропонували метод кодування, заснований на обліку умовних ймовірностей появи повідомлень. При цьому повідомленнями, які мають велику ймовірність ставилися у відповідність коротші кодові повідомлення, ніж соообщенія, мають меншу ймовірність.
Ідеї статистичного кодування отримали свій подальший розвиток в роботах Хаффмена. Код Хаффмена більш ефективний ніж Шеннона-Фано і в даний час широко використовується при побудові різноманітних программупаковщіков.
Алгоритмічне і комбинаторное кодування.
Основна ідея комбінаторного кодування полягає в завданні безлічі кодованих повідомлень не за допомогою перерахування всіх елементів безлічі, а шляхом визначення процедури обчислення номери для деякого повідомлення.
Описувані нижче методи нумеруються кодування відносяться саме до цієї групи.
В згідно з нашим методу кодування лежить метод поліадіческіх чисел, описаний в книзі В.І. Амелькина [3]. Метод поліадіческіх чисел використовує поліадіческіх систему числення, тобто таку позиційну систему числення, в якій в якості підстави прийняті не постійні числа p, а набір деяких цілих чисел l 1, l 2,..., l m, на різницю яких не накладається ніяких обмежень, т. е. l i - l j при i = j може бути більше нуля, дорівнює нулю або менше нуля [4].
У такій системі числення число L 1, a 2,..., a m можна представити у вигляді:
L = a 1 * l 2 * l 3 * ... * l m + a 2 * l 3 * l 4 * ... * l m + a m -1 * l m + a m (3)
При цьому кожна цифра a i
-
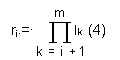
В роботі В.І. Амелькина [5] сформульована теорема існування і єдиності такого розкладу.
Використання поліадіческіх системи числення дозволяє побудувати наступний алгоритм упаковки. Нехай задана целочисленная матриця A = ai, j, i = 1, .., m, j = 1, .., n.
За допомогою перетворення
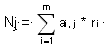
де
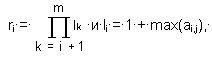
цю матрицю можна замінити двома векторами N = n j і L = l i, причому існує зворотне перетворення
a i, j = [n j / r i] - [n j / (l j * ri)] * l i, (6)
що дозволяє по N і L відновити будь-який елемент ai, j з похибкою E = 0. (Квадратними дужками тут позначена операція виділення цілої частини). Так як для зберігання векторів N і L потрібно менше двійкових одиниць, ніж для зберігання споконвічної матриці, коефіцієнт стиснення
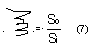
виявляється більше одиниці. Тут So- число двійкових одиниць, необхідних для зберігання вихідної матриці, Si- число двійкових одиниць, необхідних для зберігання елементів векторів N і L.
Як показали наведені нами чисельні експерименти, описаний вище алгоритм не володіє високою ефективністю. До його недоліків можна також віднести складності, що виникають при реалізації програм-пакувальників на його основі.
У зв'язку з цим, ми поставили перед собою завдання вдосконалення описаного алгоритму з метою підвищення його ефективності та створення таких його версій, які легко реалізовувалися б у вигляді програм.
У нашому алгоритмі кодується інформація може надаватися у вигляді безлічі значень змінних байтового типу. Значення об'єднані в групи по чотири числа. Нехай таких груп у вихідному інформаційному масиві виділено m (m >> 4).
Виконавши для зазначеного масиву описану вище процедуру кодування, отримаємо два вектора - N з m елементами і L, що складається з 4-х елементів.
Для підвищення ефективності алгоритму (а під ефективністю ми тут і надалі розуміємо, в першу чергу, підвищення коефіцієнта стиснення), виконаємо наступне перетворення.
Кожен з елементів отриманого вектора N представимо у вигляді 4-х розрядного двухсотпятідесятішестірічного числа і до отриманої 4-х малої матриці знову застосуємо процедуру поліадііческого кодування.
Багаторазово повторивши описану послідовність кроків, можна суттєво підвищити коефіцієнт стиснення вихідної інформації. У наведених нижче таблицях показані етапи стиснення вихідної інформації, що представляє собою деякий набір латинських літер.
Таблиці розраховувалися за допомогою табличного процесора з інтегрованого пакету Works 2.0.
Наведений приклад підтверджує високу ефективність описаного алгоритму.
Очевидно також, що на базі описуваного підходу можуть бути реалізовані швидкі і ефективні програми-пакувальники.
Таблиця 1. Приклад нумераційного кодування
Вихідний масив Компоненти вектора L
87 89 .................................. 79 89 90
90 85 .................................. 85 66 91
85 66 .................................. 78 79 86
94 80 .................................. 70 72 95
65425359 66869630 59435990 66715627 <- Вектор N
перша ітерація
3 3 ................................... 3 3 4
230 252 ................................. 138 249 253
79 89 ................................. 235 255 256
207 126 ................................. 214 235 236
59770275 61101706 54248612 60959743 <- Вектор N
восьма ітерація
0 0 .................................... 0 0 1
228 234 .................................. 210 233 235
124 188 .................................... 9 245 246
163 138 .................................... 0 255 256
14390435 14784650 13227264 14736383 <- Вектор N
Список літератури
1.І.І. Грицьків. Поняття інформації (логіко методологічний аспект). М. 1973.
2.В.А. Амелькин Методи нумераційного кодування. Новосибірськ, 1986.
3.В.А. Амелькин Методи нумераційного кодування. Новосибірськ, 1986.
4.Там ж.
5.В.А. Амелькин Методи нумераційного кодування. Новосибірськ
|